题目内容
15.反比例函数y=$\frac{-2}{x}$的图象上点A(2,m)到原点的距离AO等于( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{2}$ |
分析 先把点A(2,m)代入反比例函数y=$\frac{-2}{x}$,求出m的值,再由勾股定理即可得出结论.
解答 解:∵点A(2,m)在反比例函数y=$\frac{-2}{x}$的图象上,
∴2m=-2,解得m=-1,
∴A(2,-1),
∴OA=$\sqrt{{2}^{2}+(-1)^{2}}$=$\sqrt{5}$.
故选B.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
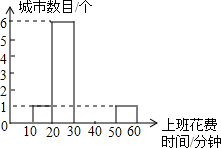
3.随着我国汽车产业的发展,城市道路拥堵问题日益严峻.某部门对15个城市的交通状况进行了调查,得到的数据如表所示:
(1)根据上班花费时间,将下面的频数分布直方图补充完整;
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.
| 城市 项目 | 北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南遇 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间(分钟) | 52 | 33 | 34 | 34 | 48 | 45 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间(分钟) | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.

4.已知一个圆锥形零件的高线为$\sqrt{5}$,底面圆半径为2,则它的侧面积为( )
| A. | 2$\sqrt{5}$ | B. | 2π | C. | 6π | D. | 3$\sqrt{5}$π |
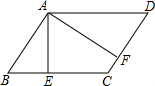 如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.
如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.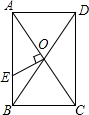 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.