题目内容
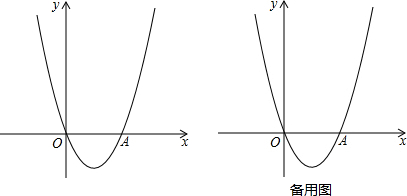
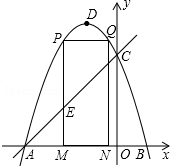
13.如图,在平面直角坐标系中,点O为坐标原点,A点的坐标为为(4,0),抛物线y=ax2-2x经过点A.(1)求抛物线的解析式;
(2)点E从点0出发沿y轴正方向以每秒1个单位长度的速度匀速运动,过点E作x轴的平行线交抛物线于C,D两点,点C在左,点D在右.设运动时间为t(t>0),设线段CD的长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,连接OC、OD,点F为OE上一点,若tan∠DOC=$\frac{CD}{OF}$,当EC=EF时,求此时D点的坐标.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据自变量与函数值的对应关系,可得关于x的方程,根据根与系数的关系,完全平方公式,可得答案;
(3)根据解方程,可得C、D点坐标,根据正切函数,可得tan∠COE,tan∠DOE,根据正切函数的和差,可得tan∠DOC,可得关于t的方程,根据解方程,可得答案.
解答 解:(1)将A点坐标代入函数解析式,得
16a-8=0,
解得a=$\frac{1}{2}$.
抛物线的解析式为y=$\frac{1}{2}$x2-2x;
(2)由题意,得
E(0,t).∵CD∥x轴,
∴C、D的纵坐标为t.
当y=t时,$\frac{1}{2}$x2-2x=t,
化简,得
$\frac{1}{2}$x2-2x-t=0,
设方程的两根为x1,x2,
由根与系数的关系,得x1+x2=4,x1•x2=-2t..
d=|x1-x2|.
d2=(x1-x2)2=(x1+x2)2-4x1x2=16+8t,
d=2$\sqrt{4+2t}$;
(3)由x2-4x-2t=0,得
x1=2+$\sqrt{4+2t}$,x2=2-$\sqrt{4+2t}$.
即C(2-$\sqrt{4+2t}$,t),D(2+$\sqrt{4+2t}$,t).CE=$\sqrt{4+2t}$-2,DE=$\sqrt{4+2t}$+2.
由CD∥x轴,得∠CEO=∠DEO=90°.
tan∠COE=$\frac{CE}{OE}$=$\frac{\sqrt{4+2t}-2}{t}$,tan∠DOE=$\frac{ED}{OE}$=$\frac{\sqrt{4+2t}+2}{t}$.
tan∠DOC=tan(∠DOE+∠COE)=$\frac{tan∠DOE+tan∠COE}{1-tan∠DOE•tan∠COE}$=$\frac{2\sqrt{4+2t}}{t-2}$.
又tan∠DOC=$\frac{CD}{OF}$=$\frac{2\sqrt{4+2t}}{OF}$.
∴$\frac{2\sqrt{4+2t}}{OF}$=$\frac{2\sqrt{4+2t}}{t-2}$,
∴OF=t-2.EF=t-(t-2)=2.
由EC=EF,即$\sqrt{4+2t}$-2=2.
解得t=6,
$\sqrt{4+2t}$+2=4+2=6,
D点的坐标为(6,6).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用完全平方公式得出d2=(x1-x2)2=(x1+x2)2-4x1x2是解题关键;利用正切函数的和差得出关于t的方程是解题关键.

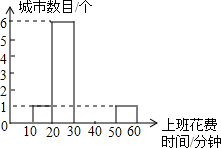
| 城市 项目 | 北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南遇 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间(分钟) | 52 | 33 | 34 | 34 | 48 | 45 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间(分钟) | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.
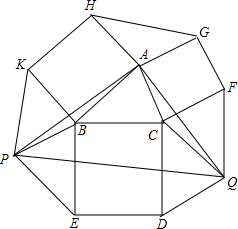 如图,已知△ABC,分别以AB、AC、BC作边作正方形ABKH、正方形ACFG、正方形BCDE,作?BEPK,?CDQF,联结AP,AQ,PQ,求证:△APQ是等腰直角三角形.
如图,已知△ABC,分别以AB、AC、BC作边作正方形ABKH、正方形ACFG、正方形BCDE,作?BEPK,?CDQF,联结AP,AQ,PQ,求证:△APQ是等腰直角三角形. 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠FEC=56°,则∠AED=62°.
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠FEC=56°,则∠AED=62°.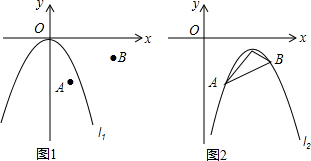
 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.