题目内容
9.(1)计算$\sqrt{18}$+$\frac{1}{\sqrt{3}}$-$\sqrt{12}$+$\sqrt{2}$;(2)化简 $\sqrt{{a}^{2}-4a+4}$+|a-1|,其中1<a<$\sqrt{2}$.
分析 根据二次根式的性质把原式化简,合并同类二次根式即可.
解答 解:(1)原式=3$\sqrt{2}$+$\frac{\sqrt{3}}{3}$-2$\sqrt{3}$+$\sqrt{2}$=4$\sqrt{2}$-$\frac{5}{3}$$\sqrt{3}$,
(2)∵1<a<$\sqrt{2}$,
∴原式=$\sqrt{(a-2)^{2}}$+a-1=2-a+a-1=1.
点评 本题考查的是二次根式的混合运算,掌握二次根式的性质是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
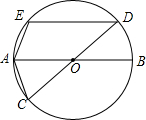 如图,AB、CD都是⊙O的直径,弦DE∥AB,
如图,AB、CD都是⊙O的直径,弦DE∥AB, 已知,如图,某长方形广场的四角都有一块边长为x米的正方形草地,若长方形的长为a米,宽为b米.
已知,如图,某长方形广场的四角都有一块边长为x米的正方形草地,若长方形的长为a米,宽为b米. 如图所示,求∠1的大小.
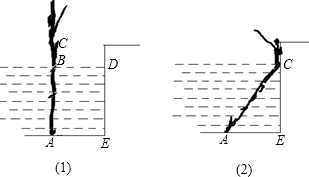
如图所示,求∠1的大小. 葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m时,这段葛藤的长是( )m.
葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m时,这段葛藤的长是( )m.