题目内容
13．
如图所示，若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，则k的取值范围是（ ）| A． | k＜-3 | B． | k＞-3 | C． | k＜3 | D． | k＞3 |
分析 根据给定图形花出函数y=|ax2+bx+c|的图象，再结合y=k与y=|ax2+bx+c|的图象有两个交点，即可得出k的取值范围．
解答 解：依照题意画出y=|ax2+bx+c|的图象，如图所示．
∵y=k与y=|ax2+bx+c|的图象有两个交点，
∴k＞3．
故选D．
点评 本题考查了抛物线与x轴的交点，解题的关键是画出函数y=|ax2+bx+c|的图象，利用数形结合解决问题．本题属于基础题，难度不大，解决该题型题目时，画出图形利用数形结合解决问题是关键．
练习册系列答案
相关题目
3．如图，在平面直角坐标系中，坐标原点O是正方形OABC的一个顶点，已知点B坐标为（1，7），过点P（a，0）（a＞0）作PE⊥x轴，与边OA交于点E（异于点O、A），将四边形ABCE沿CE翻折，点A′、B′分别是点A、B的对应点，若点A′恰好落在直线PE上，则a的值等于（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | 3 |
电子跳蚤游戏盘如图所示的△ABC，AB=8，AC=9，BC=10，如果跳蚤开始时在BC边的点P0处，BP0=4．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1=CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2=AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3=BP2；跳蚤按上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2015与A间的距离为（ ）
8．
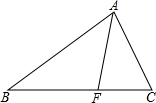如图△ABC中，AF平分∠BAC，F是BC上的一点，且BF=2CF，AC=1，则AB=（ ）
如图△ABC中，AF平分∠BAC，F是BC上的一点，且BF=2CF，AC=1，则AB=（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 6 |
有一长32厘米，宽14厘米的铁皮，若要用该铁皮做一个有盖盒子，若去掉四个角后剩余面积是整个面积的$\frac{1}{7}$，则盒子的高应为多少？
如图，△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为40°．
如图，△ABC中，∠C=90°，AC=3，AB=5，D为AB边上一点，DE∥AC，交BC于点E，DF∥BC，交AC于点F，连接EF，则线段EF的最小值为2.4．