题目内容
8.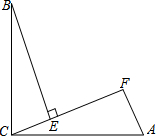 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.(1)求证:△BEC≌△CFA;
(2)若AF=5,EF=8,求BE的长;
(3)连接AB,取AB的中点为Q,连接QE,QF,判断△QEF的形状,并说明理由.
分析 (1)首先证明∠B=∠ACF,即可根据AAS证明两三角形全等.
(2)由△BEC≌△CFA,推出AF=CE=5,BE=CF,由CF=CE+EF=5+8=13,即可解决问题.
(3)△QEF是等腰直角三角形.如图,由此EQ交AF的延长线于M.只要证明△BQE≌△AQM,即可解决问题.
解答 (1)证明:∵∠BCA=∠BEC=∠F=90°,
∴∠BCE+∠B=90°,∠BCE+∠ACF=90°,
∴∠B=∠ACF,
在△BEC和△CFA中,
$\left\{\begin{array}{l}{∠B=∠ACF}\\{∠BEC=∠F}\\{BC=AC}\end{array}\right.$,
∴△BEC≌△CFA.
解:(2)∵△BEC≌△CFA,
∴AF=CE=5,BE=CF,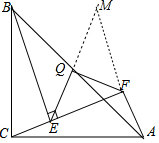
∵CF=CE+EF=5+8=13,
∴BE=13.
(3)结论:△QEF是等腰直角三角形.
理由:如图,由此EQ交AF的延长线于M.
∵BE⊥CF,AF⊥CF,
∴BE∥AM,
∴∠BEQ=∠M,
在△BQE和△AQM中,
$\left\{\begin{array}{l}{∠BEQ=∠M}\\{∠BQE=∠AQM}\\{BQ=AQ}\end{array}\right.$,
∴△BQE≌△AQM,
∴EQ=QM,BE=AM=CF,
∵CE=AF,
∴FE=FM,
∴FQ⊥EM,QF=QM=QE,
∴△QEF是等腰直角三角形.
点评 本题考查全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是学会解题常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
3.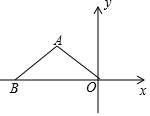 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
 如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )
如图,已知等腰△ABO的底边BO在x轴上,且BO=8,AB=AO=5,点A的坐标是( )| A. | (-3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
13.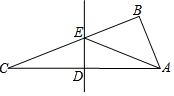 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
 如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
20.点M(cos30°,sin30°)关于原点中心对称的点的坐标是( )
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
18.下列四个图形中,线段BE是△ABC的高的是( )
| A. | 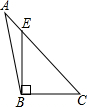 | B. | 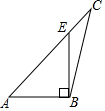 | C. | 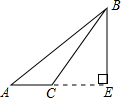 | D. | 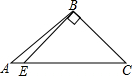 |