题目内容
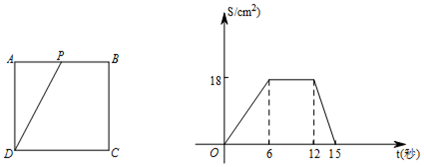
18.正方形ABCD的边长为2,P为平面内一点,△PAB,△PBC,△PCA均为等腰三角形,则△PAB的面积为2$\sqrt{2}$.分析 这样的点P有两个.由题意PA=BA=BP′=BC,可知S△ABP=S△ABP′=$\frac{1}{2}$S△APP′=$\frac{1}{2}$×PP′×OA,由此即可解决问题.
解答 解:这样的点P有两个.
∵PA=BA=BP′=BC,
∴S△ABP=S△ABP′=$\frac{1}{2}$S△APP′=$\frac{1}{2}$×PP′×OA=$\frac{1}{2}$×4×$\sqrt{2}$=2$\sqrt{2}$,
故答案为2$\sqrt{2}$.
点评 本题考查正方形的性质、等腰三角形的性质和判定.三角形的面积等知识,解题的关键是正确寻找满足条件的点P的位置,属于中考常考题型.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
3.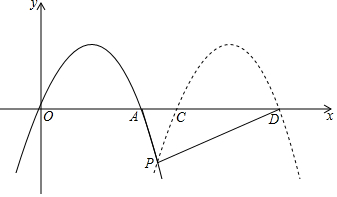 如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
 如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )
如图,抛物线y=-2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )| A. | $\frac{m}{2}$(m2-4) | B. | $\frac{1}{2}$m2-2 | C. | $\frac{m}{2}$(4-m2) | D. | 2-$\frac{1}{2}$m2 |
 如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.
如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.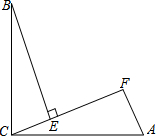 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.