题目内容
13．
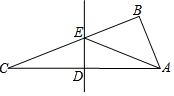如图，在△ABC中，∠ABC=90°，∠C=20°，DE是边AC的垂直平分线，连结AE，则∠BAE等于（ ）| A． | 20° | B． | 40° | C． | 50° | D． | 70° |
分析 根据三角形的内角和定理求出∠BAC，根据线段垂直平分线的性质得到EC=EA，求出∠EAC，计算即可．
解答 解：∵∠ABC=90°，∠C=20°，
∴∠BAC=70°，
∵DE是边AC的垂直平分线，
∴EC=EA，
∴∠EAC=∠C=20°，
∴∠BAE=∠BAC-∠EAC=50°，
故选：C．
点评 本题考查的是线段垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
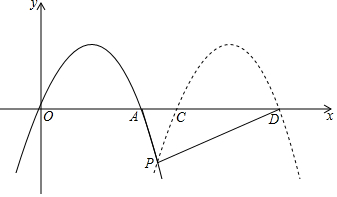如图，抛物线y=-2x2+4x与x轴的另一个交点为A，现将抛物线向右平移m（m＞2）个单位长度，所得抛物线与x轴交于C，D，与原抛物线交于点P，设△PCD的面积为S，则用m表示S正确的是（ ）
如图，抛物线y=-2x2+4x与x轴的另一个交点为A，现将抛物线向右平移m（m＞2）个单位长度，所得抛物线与x轴交于C，D，与原抛物线交于点P，设△PCD的面积为S，则用m表示S正确的是（ ）| A． | $\frac{m}{2}$（m2-4） | B． | $\frac{1}{2}$m2-2 | C． | $\frac{m}{2}$（4-m2） | D． | 2-$\frac{1}{2}$m2 |
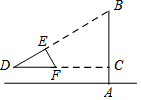如图，小南用自制的直角三角形纸板DEF测量树的高度AB，他使斜边DF保持水平，并且边DE与点B在同一直线上．己知三角形的两条直角边DE=0.6m，EF=0.3m，测得边DF离地面的高度AC=1.5m，CD=8m，求树高AB．
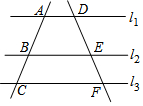如图，直线l1∥l2∥l3，直线AC依次交l1、l2、l3于A、B、C三点，直线DF依次交l1、l2、l3于D、E、F三点，若$\frac{AB}{AC}$=$\frac{4}{7}$，DE=2，求EF的长．
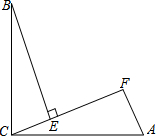如图，∠BCA=90°，AC=BC，BE⊥CF于点E，AF⊥CF于点F，其中0°＜∠ACF＜45°．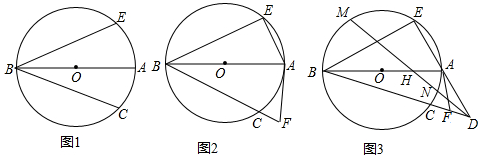
如图，点A（a，b）在第一象限，AB⊥x轴于点B．C为边0A的中点．在边OB从小于AB到大于AB的变化过程中．若a+b的值始终保持不变，则在经过动点C的反比例函数y=$\frac{k}{x}$（k≠0）中k的值的变化情况是（ ）
如图，已知等边△ABC．