题目内容
19.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:3:5,则∠D的度数为90°.分析 可设∠A=x,则∠B=3x,∠C=5x;利用圆内接四边形的对角互补,可求出∠A、∠C的度数,进而求出∠B和∠D的度数,由此得解.
解答 解:∵∠A:∠B:∠C=1:3:5,
∴设∠A=x,则∠B=3x,∠C=5x,
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,即x+5x=180,解得x=30°,
∴∠B=3x=90°,
∴∠D=180°-∠B=180°-90°=90°,
故答案为:90°.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
相关题目
14.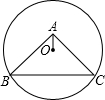 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{13}$ | C. | 4 | D. | 3$\sqrt{2}$ |
11. 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )| A. | 9.3×108 | B. | 93×107 | C. | 0.93×109 | D. | 9.3×109 |
9.G20峰会2016年9月在杭州召开之后,来杭州旅游度假的游客暴增,据统计今年国庆期间西湖风景区平均每天接待游客达到250万人,将250万用科学记数法表示,以下表示正确的是( )
| A. | 250×104 | B. | 2.5×105 | C. | 2.5×106 | D. | 2.5×107 |
 如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.
如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1=50°.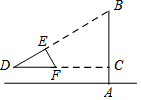 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.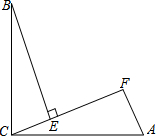 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.