题目内容
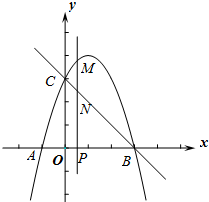 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
考点:二次函数综合题
专题:
分析:(1)把点A,点C的坐标代入抛物线y=-x2+bx+c,得出抛物线的解析式为y=-x2+2x+3,令-x2+2x+3=0,得点B的坐标(3,0),设直线BC的解析式为y=kx+b,把C(0,3),B的坐标(3,0)代入,得出直线BC的解析式为y=-x+3.
(2)由△CMN是以MN为腰的等腰直角三角形,得出CM∥x轴,即点M的纵坐标为3,把y=3代入y=-x2+2x+3,得x=0或2,由PM⊥x轴,得出点P的横坐标为m=2.
(3)由抛物线的解析式可得出M(m,-m2+2m+3),由直线BC的解析式可得N(m,-m+3),由以C、O、M、N为顶点的四边形是以OC为一边的平行四边形,可得MN=OC=3,由方程-m2+2m+3-(-m+3)=3,即可得无解.
(2)由△CMN是以MN为腰的等腰直角三角形,得出CM∥x轴,即点M的纵坐标为3,把y=3代入y=-x2+2x+3,得x=0或2,由PM⊥x轴,得出点P的横坐标为m=2.
(3)由抛物线的解析式可得出M(m,-m2+2m+3),由直线BC的解析式可得N(m,-m+3),由以C、O、M、N为顶点的四边形是以OC为一边的平行四边形,可得MN=OC=3,由方程-m2+2m+3-(-m+3)=3,即可得无解.
解答:解:(1)把点A(-1,0),点C(0,3)代入抛物线y=-x2+bx+c,得
,解得
所以抛物线的解析式为y=-x2+2x+3,
令-x2+2x+3=0,解得x1=-1,x2=3,得点B的坐标(3,0),
设直线BC的解析式为y=kx+b,把C(0,3),B的坐标(3,0)代入,得
,解得
所以直线BC的解析式为y=-x+3.
(2)∵△CMN是以MN为腰的等腰直角三角形,
∴CM∥x轴,即点M的纵坐标为3,
把y=3代入y=-x2+2x+3,得x=0或2,
∵PM⊥x轴,
∴点P的横坐标为m=2.
(3)∵抛物线的解析式为y=-x2+2x+3,P的横坐标为m
∴M(m,-m2+2m+3),
∵直线BC的解析式为y=-x+3.
∴N(m,-m+3),
∵以C、O、M、N为顶点的四边形是以OC为一边的平行四边形,
∴MN=OC=3,
∴-m2+2m+3-(-m+3)=3,化简得m2-3m+3=0,无解,
不存在m这样的值.
|
|
所以抛物线的解析式为y=-x2+2x+3,
令-x2+2x+3=0,解得x1=-1,x2=3,得点B的坐标(3,0),
设直线BC的解析式为y=kx+b,把C(0,3),B的坐标(3,0)代入,得
|
|
所以直线BC的解析式为y=-x+3.
(2)∵△CMN是以MN为腰的等腰直角三角形,
∴CM∥x轴,即点M的纵坐标为3,
把y=3代入y=-x2+2x+3,得x=0或2,
∵PM⊥x轴,
∴点P的横坐标为m=2.
(3)∵抛物线的解析式为y=-x2+2x+3,P的横坐标为m
∴M(m,-m2+2m+3),
∵直线BC的解析式为y=-x+3.
∴N(m,-m+3),
∵以C、O、M、N为顶点的四边形是以OC为一边的平行四边形,
∴MN=OC=3,
∴-m2+2m+3-(-m+3)=3,化简得m2-3m+3=0,无解,
不存在m这样的值.
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 DF⊥AB于F交AC于E,∠A=30°,∠D=40°,求∠ACB的度数.
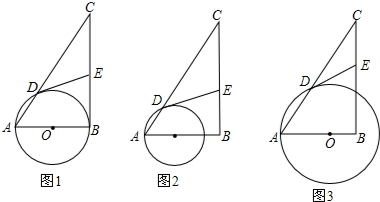
DF⊥AB于F交AC于E,∠A=30°,∠D=40°,求∠ACB的度数. 已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°-
已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°- 如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.
如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.
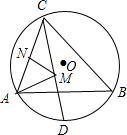 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值. 已知:AB=AC,AD=DE,BE∥AD,AD=DE,求证:∠BED=∠BAD.
已知:AB=AC,AD=DE,BE∥AD,AD=DE,求证:∠BED=∠BAD.