题目内容
 已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°-
已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°-| 1 |
| 2 |
考点:切线的性质
专题:
分析:作出辅助线,运用切线的性质构造全等三角形,证明∠COD=
∠AOB,即可解决问题.
| 1 |
| 2 |
解答:证明:如图,连接OA、OB、OE;
∵CA、CE分别是⊙O的切线,
∴∠CAE=∠CEO=90°,CE=CA;
在△COA与△COE中,
,
∴△COA≌△COE(HL),
∴∠COE=∠COA;
同理可证∠DOE=∠DOB,
∴∠COD=
∠AOB;
∵OA⊥PA,OB⊥PB,
∴∠AOB+∠P=180°,
∴∠AOB=180°-∠P
∴∠COD=90°-
∠P.
∵CA、CE分别是⊙O的切线,
∴∠CAE=∠CEO=90°,CE=CA;
在△COA与△COE中,
|
∴△COA≌△COE(HL),
∴∠COE=∠COA;

同理可证∠DOE=∠DOB,
∴∠COD=
| 1 |
| 2 |
∵OA⊥PA,OB⊥PB,
∴∠AOB+∠P=180°,
∴∠AOB=180°-∠P
∴∠COD=90°-
| 1 |
| 2 |
点评:该题考查了切线的性质及其应用问题;解题的关键是作辅助线构造全等三角形,灵活运用切线的性质解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=
如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=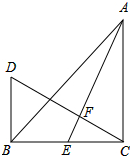 如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.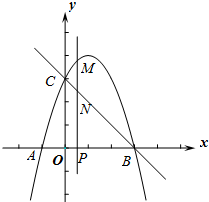 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m. 如图,两个同心圆中,弦AB和小圆相切,且AB=12,∠COD=120°,则图中阴影部分的面积为
如图,两个同心圆中,弦AB和小圆相切,且AB=12,∠COD=120°,则图中阴影部分的面积为