题目内容
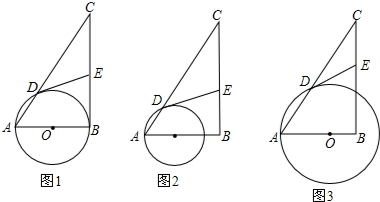
已知:在△ABC中,AB=6,BC=8,AC=10,O为AB边上的一点,以O为圆心,OA长为半径作圆交AC于点D,过D作⊙O的切线交BC于点E.
(1)若O为AB的中点(如图1),则ED与EC的大小关系为:ED EC.(填“>““<““=“)
(2)若OA<3时(如图2),(1)中的关系是否还成立?为什么?
(3)当⊙O过BC中点时(如图3),求CE长.
(1)若O为AB的中点(如图1),则ED与EC的大小关系为:ED
(2)若OA<3时(如图2),(1)中的关系是否还成立?为什么?
(3)当⊙O过BC中点时(如图3),求CE长.

考点:圆的综合题
专题:
分析:(1)连接OD,根据切线的性质可得∠ODE=90°,则∠CDE+∠ADO=90°,由AB=6,BC=8,AC=10根据勾股定理的逆定理可证得∠ABC=90°,则∠A+∠C=90°,根据圆的基本性质可得∠A=∠ADO,即可得到∠CDE=∠C,从而证得结论;
(2)证法同(1);
(3)根据直角三角形的性质结合圆的基本性质,先求出圆的半径,再结合前两问的结论,在Rt△DEF中,利用勾股定理求解即可.
(2)证法同(1);
(3)根据直角三角形的性质结合圆的基本性质,先求出圆的半径,再结合前两问的结论,在Rt△DEF中,利用勾股定理求解即可.
解答:解:(1)如图1,连接OD,

∵DE为⊙O的切线,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
∵AB=6,BC=8,AC=10,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵AO=DO,
∴∠A=∠ADO,
∴∠CDE=∠C,
∴ED=EC,
故答案为:=;
(2)如图2,连接OD,

∵DE为⊙O的切线,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
∵AB=6,BC=8,AC=10,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵AO=DO,
∴∠A=∠ADO,
∴∠CDE=∠C,
∴ED=EC;
(3)设BC中点为F,如图3,连接OF、OD、OE,

设OA=r,则OB=6-r,且BF=4,
在Rt△OBF中,由勾股定理可得:OF2=OB2+BF2,即r2=(6-r)2+42,解得r=
,
设CE=DE=x,则BE=8-x,在Rt△OBE中,由勾股定理可得:OE2=OB2+BE2,
则在Rt△ODE中,由勾定理可得:OE2=OD2+DE2,
∴OB2+BE2=OD2+DE2,即(6-r)2+(8-x)2=r2+x2,
整理可得3r+4x=25,把r=
代入可得x=3,
即CE长为3.

∵DE为⊙O的切线,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
∵AB=6,BC=8,AC=10,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵AO=DO,
∴∠A=∠ADO,
∴∠CDE=∠C,
∴ED=EC,
故答案为:=;
(2)如图2,连接OD,

∵DE为⊙O的切线,
∴∠ODE=90°,
∴∠CDE+∠ADO=90°,
∵AB=6,BC=8,AC=10,
∴∠ABC=90°,
∴∠A+∠C=90°,
∵AO=DO,
∴∠A=∠ADO,
∴∠CDE=∠C,
∴ED=EC;
(3)设BC中点为F,如图3,连接OF、OD、OE,

设OA=r,则OB=6-r,且BF=4,
在Rt△OBF中,由勾股定理可得:OF2=OB2+BF2,即r2=(6-r)2+42,解得r=
| 13 |
| 3 |
设CE=DE=x,则BE=8-x,在Rt△OBE中,由勾股定理可得:OE2=OB2+BE2,
则在Rt△ODE中,由勾定理可得:OE2=OD2+DE2,
∴OB2+BE2=OD2+DE2,即(6-r)2+(8-x)2=r2+x2,
整理可得3r+4x=25,把r=
| 13 |
| 3 |
即CE长为3.
点评:本题主要考查圆的切线的性质及圆的基本性质、勾股定理等的综合应用,一般出现切点连接圆心和切点是常用的辅助线,再结合直角三角形进行求解即可.

练习册系列答案
相关题目
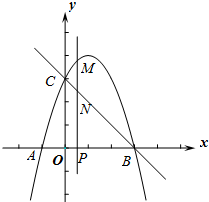 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m. 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6.