题目内容
如图，△ABC中，∠ACB=120°，∠A=20°，CD⊥AB于D，试探究BC、BD、AD之间的关系．考点：全等三角形的判定与性质
专题：
分析：如图，在AD上取一点E，使DE=DB，构建全等三角形：△CED≌△CBD，则由该全等三角形的性质推知BC=EC，然后根据等腰三角形的判定与性质得到AE=EC，则AD=AE+ED=BC+BD．
解答：
解：BC+BD=AD．理由如下：
∵CD⊥AB，
∴∠ADC=∠BDC=90°．
又∵∠A=20°，
∴∠ACD=70°．
∵∠ACB=120°，
∴∠BCD=50°，
则∠B=40°．
如图，在AD上取一点E，使DE=DB．
在△CED与△CBD中，
，
∴△CED≌△CBD（SAS），
∴CE=CB，∠CEB=∠B=40°．
又∵∠CEB=∠A+∠ACE=20°+∠ACE=40°，
∴∠ACE=20°，则∠A=∠ACE，
∴AE=EC，
∴AE=EC=BC，
∴AE+ED=BC+BD=AD，即BC+BD=AD．
解：BC+BD=AD．理由如下：∵CD⊥AB，
∴∠ADC=∠BDC=90°．
又∵∠A=20°，
∴∠ACD=70°．
∵∠ACB=120°，
∴∠BCD=50°，
则∠B=40°．
如图，在AD上取一点E，使DE=DB．
在△CED与△CBD中，
|
∴△CED≌△CBD（SAS），
∴CE=CB，∠CEB=∠B=40°．
又∵∠CEB=∠A+∠ACE=20°+∠ACE=40°，
∴∠ACE=20°，则∠A=∠ACE，
∴AE=EC，
∴AE=EC=BC，
∴AE+ED=BC+BD=AD，即BC+BD=AD．
点评：本题是简单的推理证明题，主要考查直角三角形的性质，同时综合利用全等三角形的判定方法及等腰三角形的性质推知相关线段间的数量关系．
练习册系列答案
相关题目
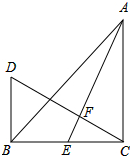如图，在△ABC中，∠ACB=90°，AC=BC，AE是BC的中线，过点C作CF⊥AE于F，过B作BD⊥CB交CF的延长线于点D．
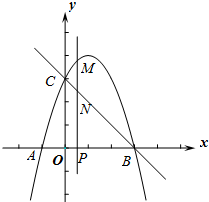如图，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（-1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．