题目内容
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点D、E、F分别是边AB、BC、AC的中点,连接DE、DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿A-F-D的方向运动到点D停止;点Q沿B-C的方向运动,当点P停止运动时,点Q也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0有几何图形),点P运动的时间为x(s)
(1)当点P运动到点F时,CQ= cm,MQ= cm;
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关系式.

(1)当点P运动到点F时,CQ=
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关系式.

考点:四边形综合题
专题:
分析:(1)当点P运动到点F时,求出AF=FC=3cm,BQ=AF=3cm,PQ∥AC,可得出
=
,代入可求出MQ,得出答案;
(2)根据在点P从点F运动到点D的过程中,点P落在MQ上得出方程t+t-3=8,求出即可;
(3)求出DE=
AC=3,DF=
BC=4,证△MBQ∽△ABC,求出MQ=
x,分为三种情况:①当3≤x<4时,重叠部分图形为平行四边形,根据y=PN•PD代入求出即可;②当4≤x<
时,重叠部分为矩形,根据图形得出y=3[(8-x)-(x-3)];③当
≤x≤7时,重叠部分图形为矩形,根据图形得出y=3[(x-3)-(8-x)],求出即可.
| MQ |
| AC |
| BQ |
| BC |
(2)根据在点P从点F运动到点D的过程中,点P落在MQ上得出方程t+t-3=8,求出即可;
(3)求出DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 11 |
| 2 |
| 11 |
| 2 |
解答:解:(1)当点P运动到点F时,
∵F为AC的中点,AC=6cm,
∴AF=FC=3cm,
∵P和Q的运动速度都是1cm/s,
∴BQ=AF=3cm,
∴CQ=8cm-3cm=5cm,
∵MQ⊥BC,∠ACB=90°,
∴MQ∥AC,
∴
=
,
即
=
,
∴MQ=
,
故答案为:5;
;
(2) 设在点P从点F运动到点D的过程中,点P落在MQ上,如图1,
设在点P从点F运动到点D的过程中,点P落在MQ上,如图1,
则x+x-3=8,
x=
,
BQ的长度为
×1=
(cm);
(3)∵D、E、F分别是AB、BC、AC的中点,
∴DE=
AC=
×6=3,
DF=
BC=
×8=4,
∵MQ⊥BC,
∴∠BQM=∠C=90°,
∵∠QBM=∠CBA,
∴△MBQ∽△ABC,
∴
=
,
∴
=
,MQ=
x,
分为三种情况:
①当3≤x<4时,重叠部分图形为平行四边形,如图2,
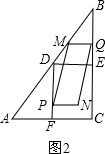
y=PN•PD=
x(7-x),y=-
x2+
x;
②当4≤x<
时,重叠部分为矩形,如图3,
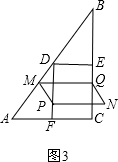
y=3[(8-x)-(x-3)],即y=-6x+33;
③当
≤x≤7时,重叠部分图形为矩形,如图4,
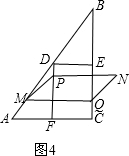
y=3[(x-3)-(8-x)],即y=6x-33,
综上所述,当3≤x<4时,y=-
x2+
,
当4≤x<
时,y=-6x+33;
当
≤x≤7时,y=6x-33,
所以y与x之间的函数关系式是:y=
.
∵F为AC的中点,AC=6cm,
∴AF=FC=3cm,
∵P和Q的运动速度都是1cm/s,
∴BQ=AF=3cm,
∴CQ=8cm-3cm=5cm,
∵MQ⊥BC,∠ACB=90°,
∴MQ∥AC,
∴
| MQ |
| AC |
| BQ |
| BC |
即
| MQ |
| 6 |
| 3 |
| 8 |
∴MQ=
| 9 |
| 4 |
故答案为:5;
| 9 |
| 4 |
(2)
 设在点P从点F运动到点D的过程中,点P落在MQ上,如图1,
设在点P从点F运动到点D的过程中,点P落在MQ上,如图1,则x+x-3=8,
x=
| 11 |
| 2 |
BQ的长度为
| 11 |
| 2 |
| 11 |
| 2 |
(3)∵D、E、F分别是AB、BC、AC的中点,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
DF=
| 1 |
| 2 |
| 1 |
| 2 |
∵MQ⊥BC,
∴∠BQM=∠C=90°,
∵∠QBM=∠CBA,
∴△MBQ∽△ABC,
∴
| BQ |
| BC |
| MQ |
| AC |
∴
| x |
| 8 |
| MQ |
| 6 |
| 3 |
| 4 |
分为三种情况:
①当3≤x<4时,重叠部分图形为平行四边形,如图2,

y=PN•PD=
| 3 |
| 4 |
| 3 |
| 4 |
| 21 |
| 4 |
②当4≤x<
| 11 |
| 2 |

y=3[(8-x)-(x-3)],即y=-6x+33;
③当
| 11 |
| 2 |

y=3[(x-3)-(8-x)],即y=6x-33,
综上所述,当3≤x<4时,y=-
| 3 |
| 4 |
| 21 |
| 4 |
当4≤x<
| 11 |
| 2 |
当
| 11 |
| 2 |
所以y与x之间的函数关系式是:y=
|
点评:本题主要考查了函数的应用及矩形、平行四边形的性质和三角形的中位线的综合应用,主要考查学生综合运用性质进行计算的能力,在第(3)中正确分类讨论是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=APi2+BPi•PiC(i=1,2…100),则m1+m2+…+m100的值是( )
如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=APi2+BPi•PiC(i=1,2…100),则m1+m2+…+m100的值是( )| A、300 | B、400 |
| C、800 | D、900 |
比较下列三个数-0.25,-
,-0.3的大小关系为( )
| 1 |
| 2 |
A、-0.25<-
| ||
B、-0.25<-0.3<-
| ||
C、-
| ||
D、-
|
 如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D. 如图,五边形ABCDE中,∠E=∠B=90°,DE+BC=2,DC=AB=AE=2,求这个五边形的面积.
如图,五边形ABCDE中,∠E=∠B=90°,DE+BC=2,DC=AB=AE=2,求这个五边形的面积.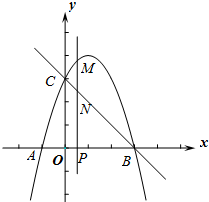 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.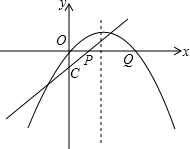 已知直线y=
已知直线y= 如图,圆O内切于△ABC,交AB、AC于D、E两点,已知∠A=60°,BC=7,S△ABC=20.求DE的长.
如图,圆O内切于△ABC,交AB、AC于D、E两点,已知∠A=60°,BC=7,S△ABC=20.求DE的长.