题目内容
DF⊥AB于F交AC于E，∠A=30°，∠D=40°，求∠ACB的度数．考点：三角形内角和定理
专题：
分析：先根据直角三角形的性质求出∠AEF的度数，进而可得出∠CED的度数，由三角形外角的性质即可得出结论．
解答：解：∵DF⊥AB，
∴∠AFE=90°．
∵∠A=30°，
∴∠AEF=90°-30°=60°．
∵∠AEF与∠CED是对顶角，
∴∠CED=60°．
∵∠ACB是△AED的外角，
∴∠ACB=∠D+∠CED=40°+60°=100°．
∴∠AFE=90°．
∵∠A=30°，
∴∠AEF=90°-30°=60°．
∵∠AEF与∠CED是对顶角，
∴∠CED=60°．
∵∠ACB是△AED的外角，
∴∠ACB=∠D+∠CED=40°+60°=100°．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
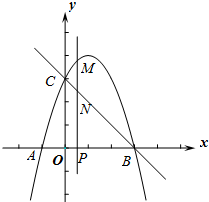如图，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（-1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．