题目内容
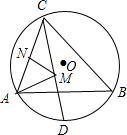 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.考点:轴对称-最短路线问题
专题:
分析:连接OA,OC,过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,则A′N′的长即为MA+MN的最小值.
解答: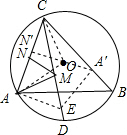 解:连接OA,OC,
解:连接OA,OC,
∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
=
=2
.
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵CD平分∠ACB交⊙O于D,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
,
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
×
=
,即MA+MN的最小值是
.
 解:连接OA,OC,
解:连接OA,OC,∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
| 2OA2 |
| 2×4 |
| 2 |
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵CD平分∠ACB交⊙O于D,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
| 2 |
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
| 2 |
| ||
| 2 |
| 6 |
| 6 |
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列说法正确的是( )
| A、“明天降雨的概率是50%”表示明天有半天都在降雨 | ||||||||
| B、数据4,4,5,5,0的中位数和众数都是5 | ||||||||
| C、要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式 | ||||||||
D、若甲、乙两组数中各有20个数据,平均数
|

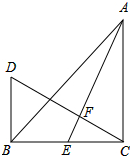 如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.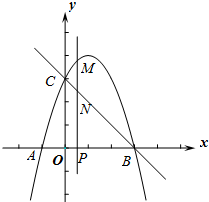 如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(-1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.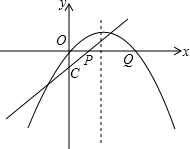 已知直线y=
已知直线y= 如图,圆O内切于△ABC,交AB、AC于D、E两点,已知∠A=60°,BC=7,S△ABC=20.求DE的长.
如图,圆O内切于△ABC,交AB、AC于D、E两点,已知∠A=60°,BC=7,S△ABC=20.求DE的长. 如图,两个同心圆中,弦AB和小圆相切,且AB=12,∠COD=120°,则图中阴影部分的面积为
如图,两个同心圆中,弦AB和小圆相切,且AB=12,∠COD=120°,则图中阴影部分的面积为