题目内容
已知：AB=AC，AD=DE，BE∥AD，AD=DE，求证：∠BED=∠BAD．考点：全等三角形的判定与性质
专题：证明题
分析：作DG⊥AB于G，DH⊥EB于H，求出∠1=∠C=∠2，根据AAS证出△DGB≌△DHB，推出GD=DH，根据HL证出Rt△ADG≌Rt△EDH即可．
解答：
证明：作DG⊥AB于G，DH⊥EB于H，
则∠DGB=∠H=90°，
∵AB=AC，BE∥AC，
∠1=∠C=∠2，
在△DGB和△DHB中，
，
∴△DGB≌△DHB（AAS），
∴GD=DH，
在Rt△ADG和Rt△EDH中，
，
∴Rt△ADG≌Rt△EDH（HL），
∴∠BED=∠BAD．
证明：作DG⊥AB于G，DH⊥EB于H，则∠DGB=∠H=90°，
∵AB=AC，BE∥AC，
∠1=∠C=∠2，
在△DGB和△DHB中，
|
∴△DGB≌△DHB（AAS），
∴GD=DH，
在Rt△ADG和Rt△EDH中，
|
∴Rt△ADG≌Rt△EDH（HL），
∴∠BED=∠BAD．
点评：本题考查了全等三角形的性质和判定，平行线的性质，等腰三角形的性质的应用，解此题的关键是正确作辅助线后求出全等三角形．
练习册系列答案
相关题目
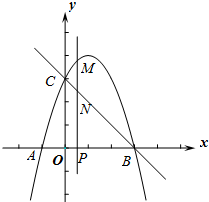如图，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（-1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．
如图，圆O内切于△ABC，交AB、AC于D、E两点，已知∠A=60°，BC=7，S△ABC=20．求DE的长．
如图，两个同心圆中，弦AB和小圆相切，且AB=12，∠COD=120°，则图中阴影部分的面积为