题目内容
15. 如图,抛物线y=-x2+3x与x轴交于一点B,顶点为A,连接BA并延长与y轴交于点C,则阴影部分的面积和为$\frac{27}{8}$.
如图,抛物线y=-x2+3x与x轴交于一点B,顶点为A,连接BA并延长与y轴交于点C,则阴影部分的面积和为$\frac{27}{8}$.
分析 根据抛物线的对称性得到图中阴影部分的面积=三角形OAC的面积.
解答 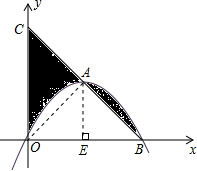 解:∵y=-x2+3x=-x(x-3)=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
解:∵y=-x2+3x=-x(x-3)=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴该抛物线经过O(0,0),B(0,3),且顶点A($\frac{3}{2}$,$\frac{9}{4}$).
又∵点A为抛物线的顶点,
∴根据抛物线的对称性得到:S阴影=S△OAC.
如图,过点A作AE⊥OB于E,则AE∥OC,
又∵点E是OB的中点,
∴点A是BC的中点,
∴AE是△OBC的中位线,
∴OC=2AE=$\frac{9}{2}$,
∴S阴影=S△OAC=$\frac{1}{2}$×$\frac{9}{2}$×$\frac{3}{2}$=$\frac{27}{8}$,
故答案是:$\frac{27}{8}$.
点评 本题考查了抛物线与x轴的交点.利用抛物线的对称性质将所求的阴影部分的面积转化为规则图形的面积是解题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
