题目内容
20.定义[a,b,c]为函数y=ax2+bx+c的“特征数”.如:函数y=x2+3x-2的“特征数”是[1,3,-2],函数y=-x+4的“特征数”是[0,-1,4].如果将“特征数”是[2,0,4]的函数图象向下平移3个单位,得到一个新函数图象,那么这个新函数的解析式是y=2x2+1.分析 根据“特征数”的定义得到:“特征数”是[2,0,4]的函数的解析式为:y=2x2+4,则该抛物线的顶点坐标是(0,4),根据平移规律得到新函数解析式.
解答 解:依题意得:“特征数”是[2,0,4]的函数解析式为:y=2x2+4,其顶点坐标是(0,4),向下平移3个单位后得到的顶点坐标是(0,1),
所以新函数的解析式为:y=2x2+1.
故答案是:y=2x2+1.
点评 主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{15}{x}$ | D. | y=-$\frac{15}{x}$ |
12.若直线y=ax+b(a≠0)在第二、四象限都无图象,则抛物线y=ax2+bx+c( )
| A. | 开口向上,对称轴是y轴 | B. | 开口向下,对称轴平行于y轴 | ||
| C. | 开口向上,对称轴平行于y轴 | D. | 开口向下,对称轴是y轴 |
9.如果点A(-4,y1),B(-1,y2),C(3,y3)都在反比例函数$y=\frac{k}{x}(k<0)$的图象上,那么y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y3<y2<y1 |

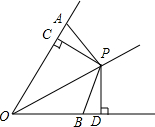 如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长.
如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长. 如图,抛物线y=-x2+3x与x轴交于一点B,顶点为A,连接BA并延长与y轴交于点C,则阴影部分的面积和为$\frac{27}{8}$.
如图,抛物线y=-x2+3x与x轴交于一点B,顶点为A,连接BA并延长与y轴交于点C,则阴影部分的面积和为$\frac{27}{8}$. 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=80°,则∠A=50°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=80°,则∠A=50°.