题目内容
5．如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有6个，第（3）个图形中面积为1的正方形有12个，…，按此规律，则第（6）个图形中面积为1的正方形的个数为（ ）
| A． | 20 | B． | 30 | C． | 42 | D． | 56 |
分析 由题意可知：第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有2+4=6个，第（3）个图形中面积为1的正方形有2+4+6=12个，…，按此规律，则第n个图形中面积为1的正方形的个数为2（1+2+3+…+n）=n（n+1），由此进一步代入求得答案即可．
解答 解：第（1）个图形中面积为1的正方形有2个，
第（2）个图形中面积为1的正方形有2+4=6个，
第（3）个图形中面积为1的正方形有2+4+6=12个，…，
第n个图形中面积为1的正方形的个数为2（1+2+3+…+n）=n（n+1），
第（6）个图形中面积为1的正方形的个数为6×7=42．
故选：C．
点评 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
12．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x-3=0}\\{3x-2y=7}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2x-y=3}\\{3xy=8}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=3}\\{x-z=5}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{3}{y}=4}\\{\frac{1}{3}x+\frac{1}{2}y=1}\end{array}\right.$ |
16．
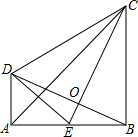如图，CB⊥AB，DA⊥AB，垂足分别是A、B，AB=BC，E是AB中点，CE⊥DB，CE交BD于点O．下列结论：①BE=AD；②AC垂直平分DE；③∠DBC=∠DCB；④∠CED=∠DBC；⑤BC=CD．其中正确的有（ ）
如图，CB⊥AB，DA⊥AB，垂足分别是A、B，AB=BC，E是AB中点，CE⊥DB，CE交BD于点O．下列结论：①BE=AD；②AC垂直平分DE；③∠DBC=∠DCB；④∠CED=∠DBC；⑤BC=CD．其中正确的有（ ）| A． | ①②③ | B． | ①③⑤ | C． | ①②④ | D． | ②③⑤ |
13．
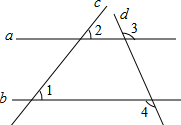如图，若∠1=40°，∠2=40°，∠3=110°36′，则∠4的度数为（ ）
如图，若∠1=40°，∠2=40°，∠3=110°36′，则∠4的度数为（ ）| A． | 68.6° | B． | 110°36′ | C． | 68.4° | D． | 69.4° |
已知三角形ABC、点D，过点D作三角形ABC平移后的图形，使D点与A点为对应点．
如图，抛物线y=-x2+3x与x轴交于一点B，顶点为A，连接BA并延长与y轴交于点C，则阴影部分的面积和为$\frac{27}{8}$．