题目内容
4．先化简，再求值：$\frac{{{x^2}+2x}}{x-1}•（{1-\frac{1}{x}}）$，其中x是不等式组$\left\{\begin{array}{l}x+4＞0\\ 2x+5＜1\end{array}$的整数解．分析 将分式化简，求出不等式组的解集，并求出整数解，将整数解代入即可．
解答 解：原式=$\frac{x（x+2）}{x-1}$•$\frac{x-1}{x}$
=x+2，
解不等式$\left\{\begin{array}{l}x+4＞0①\\ 2x+5＜1②\end{array}\right.$得，
由①得，x＞-4，
由②得，x＜-2，
不等式的解集为-4＜x＜-2，
其整数解为-3，
当x=-3时，原式=-3+2=-1．
点评 本题考查了分式的化简求值、一元一次不等式组的整数解，熟悉通分、因式分解是解题的关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
如图，抛物线y=-x2+3x与x轴交于一点B，顶点为A，连接BA并延长与y轴交于点C，则阴影部分的面积和为$\frac{27}{8}$．
12．若直线y=ax+b（a≠0）在第二、四象限都无图象，则抛物线y=ax2+bx+c（ ）
| A． | 开口向上，对称轴是y轴 | B． | 开口向下，对称轴平行于y轴 | ||
| C． | 开口向上，对称轴平行于y轴 | D． | 开口向下，对称轴是y轴 |
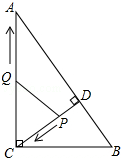如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
9．如果点A（-4，y1），B（-1，y2），C（3，y3）都在反比例函数$y=\frac{k}{x}（k＜0）$的图象上，那么y1，y2，y3的大小关系是（ ）
| A． | y1＜y3＜y2 | B． | y3＜y1＜y2 | C． | y1＜y2＜y3 | D． | y3＜y2＜y1 |
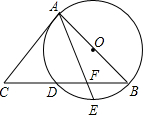如图，AB是⊙O的直径，BC交⊙O于点D，E是$\widehat{BD}$的中点，连接AE交BC于点F，∠ACB=2∠EAB．