题目内容
6.如图1,平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与抛物线y=ax2+$\frac{9}{4}$x+c相交于A,B两点,其中点A在x轴上,点B在y轴上.(1)求抛物线的解析式;
(2)在抛物线上存在一点M,使△MAB是以AB为直角边的直角三角形,求点M的坐标;
(3)如图2,点E为线段AB上一点,BE=2,以BE为腰作等腰Rt△BDE,使它与△AOB在直线AB的同侧,∠BED=90°,△BDE沿着BA方向以每秒一个单位的速度运动,当点B与A重合时停止运动,设运动时间为t秒,△BDE与△AOB重叠部分的面积为S,直接写出S关于t的函数关系式,并写出自变量t的取值范围.

分析 (1)根据直线解析式,求出A与B的坐标,代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)由M在抛物线图象上,设出M坐标,分两种情况考虑:①当∠MBA=90°时;②当∠BAM′=90°时,分别求出M坐标即可;
(3)根据t的范围,分三种情况考虑:当0≤t≤$\frac{1}{3}$时;当$\frac{1}{3}$≤t≤3时;当3≤t≤5时,分别确定出S与t的函数解析式即可.
解答 解:(1)对于直线y=-$\frac{3}{4}$x+3,
当y=0时,0=-$\frac{3}{4}$x+3,即x=4,
∴A(4,0),
当x=0时,y=3,即B(0,3),
把A与B坐标代入y=ax2+$\frac{9}{4}$x+c中,得:$\left\{\begin{array}{l}{16a+9+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{c=3}\end{array}\right.$,
则抛物线解析式为y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3;″
(2)设M坐标为(x,-$\frac{3}{4}$x2+$\frac{9}{4}$x+3),
①当∠MBA=90°时,如图1,作MN⊥y轴,则有∠MNO=90°,
∴∠NMB+∠MBN=90°,
∵∠MBN+∠ABM+∠ABO=180°,
∴∠MBN+∠ABO=90°,
∴∠NMB=∠ABO,
∵∠MNO=∠BOA,
∴△MNB∽△BOA,
∴$\frac{MN}{BO}$=$\frac{BN}{AO}$,
即$\frac{x}{3}$=$\frac{-\frac{3}{4}{x}^{2}+\frac{9}{4}x+3-3}{4}$,
解得:x=$\frac{11}{9}$或x=0(舍去),
当x=$\frac{11}{9}$时,y=$\frac{125}{27}$,即M($\frac{11}{9}$,$\frac{125}{27}$);
②当∠BAM′=90°时,易知△AM′N′∽△BAO,∴$\frac{A{N}^{′}}{BO}=\frac{M′N′}{AO}$,
即$\frac{4-x}{3}=\frac{\frac{3}{4}{x}^{2}-\frac{9}{4}x-3}{4}$,解得x=-$\frac{25}{9}$或4(舍去),当x=-$\frac{25}{9}$时,y=-$\frac{244}{27}$,
即M′(-$\frac{25}{9}$,-$\frac{244}{27}$),
则满足条件M的坐标为($\frac{11}{9}$,$\frac{125}{27}$)或(-$\frac{25}{9}$,-$\frac{244}{27}$);
(3)如图2所示,当D点运动到x轴上时,易知△AD′E′∽△ABO,
∴$\frac{AE′}{AO}=\frac{D′E′}{BO}$,∴AE′=$\frac{8}{3}$,∴EE′=AB-BE-AE′=5-2-$\frac{8}{3}$=$\frac{1}{3}$,
∴当0≤t≤$\frac{1}{3}$时,S=2;
当$\frac{1}{3}$≤t≤3时,S=-$\frac{9}{56}$t2+$\frac{3}{28}$t+$\frac{111}{56}$;
当3≤t≤5时,S=$\frac{3}{14}$t2-$\frac{15}{7}$t+$\frac{75}{14}$.
点评 此题属于二次函数综合题,涉及的知识有:一次函数与坐标轴的交点,待定系数法确定抛物线解析式,相似三角形的判定与性质,利用了分类讨论的思想,熟练掌握二次函数的性质是解本题的关键.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 无正数解 | B. | 只有一组正数解 | ||
| C. | 无正整数解 | D. | 只有一组正整数解 |
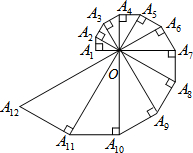 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )| A. | 22013 | B. | 22014 | C. | ($\frac{2}{\sqrt{3}}$)2013 | D. | ($\frac{2}{\sqrt{3}}$)2014 |
| A. | M=2,N=3 | B. | M=3,N=2 | C. | M=2,N=2 | D. | M=3,N=3 |