题目内容
14．已知x＞0，且$x-\frac{1}{x}$=1，求$x+\frac{1}{x}$的值．分析 把已知等式两边平方，利用完全平方公式化简，整理求出x2+$\frac{1}{{x}^{2}}$的值，再利用完全平方公式即可求出所求式子的值．
解答 解：由x-$\frac{1}{x}$=1，得到（x-$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$-2=1，即x2+$\frac{1}{{x}^{2}}$=3，
∴（x+$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$+2=3+2=5，
∵x＞0，
∴x+$\frac{1}{x}$=$\sqrt{5}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
4．如图1，在矩形ABCD中，AB=2，动点P从点B出发，沿路线B→C→D作匀速运动，图2是此运动过程中，△PAB的面积S与点P运动的路程x之间的函数图象的一部分，则BC的长为（ ）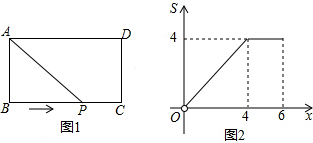
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
如图，△ABC在直角坐标系中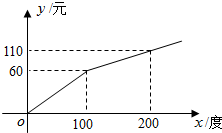
电力资源丰富，并且得到了较好的开发．某地区一家供电公司为了鼓励居民用电，采用分段计费的方法来计算电费．月用电量x（度）与相应电费y（元）之间的函数图象如图．
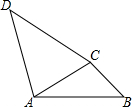如图，在四边形ABCD中，∠ACB=∠BAD=105°，∠B=∠D=45°．若AD=$\sqrt{6}$，则AB=$\sqrt{3}$+1．
19．
如图，在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°．若点A1的坐标为（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，则依次规律，点A2016的纵坐标为（ ）
如图，在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°．若点A1的坐标为（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，则依次规律，点A2016的纵坐标为（ ）| A． | 0 | B． | -3×（$\frac{2}{3}$$\sqrt{3}$）2015 | C． | （2$\sqrt{3}$）2016 | D． | 3×（$\frac{2}{3}$$\sqrt{3}$）2015 |
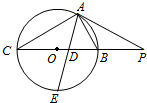如图所示，PA为圆O的切线，A为切点，PBC是过点O的割线，PA=10，PB=5，∠CAB的平分线与BC和圆O分别交于点D和E．