题目内容
15.已知:关于x的方程x2+(m-1)x-1=0,(1)求证:方程有两个不相等的实数根;
(2)设方程两个实数根分别为x1,x2,当|x1|=4|x2|时,求实数m的值.
分析 (1)根据根的判别式的符号进行证明;
(2)利用根与系数的关系得出x1+x2=1-m,x1x2=1,分x1=4x2,x1=-4x2,分类探讨得出答案即可.
解答 解:(1)∵△=(m-1)2-4×(-1)=(m-1)2+4>0,
∴关于x的方程x2+(m-1)x-1=0有两个不相等的实数根;
(2)设方程两个实数根分别为x1,x2,
则x1+x2=1-m,x1x2=1,
∵|x1|=4|x2|,
∴x1=±4x2,
当x1=4x2时
$\left\{\begin{array}{l}{5{x}_{2}=1-m}\\{4{x}_{2}^{2}=1}\end{array}\right.$
解得m=-2,或m=3;
当x1=-4x2时
$\left\{\begin{array}{l}{-3{x}_{2}=1-m}\\{-4{x}_{2}^{2}=-1}\end{array}\right.$,舍去.
∴m=-2,或m=3.
点评 本题考查了一元二次方程根的判别式和根与系数的关系,(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根;根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
20.下列几何体中主视图、左视图、俯视图都相同的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中
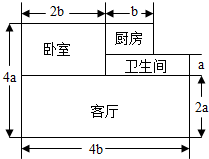 李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔买了一套新房,其结构如图(单位:m),他打算除卧室外,其余部分铺地砖.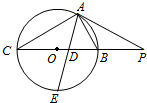 如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.