题目内容
10.已知:∠1=∠2,3=∠4,过点P作PD∥BC交直线AB于点D,交直线AC于点H,PK∥AC交直线BC于点K,请你解答下列问题: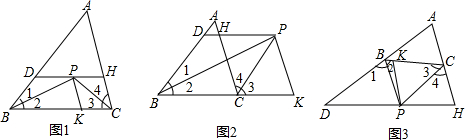
(1)如图1,求证:BD=DH-PK;
(2)如图2、3,DH、PK又有怎样的数量关系?直接写出你的猜想,不需要证明;
(3)在(1)(2)的条件下,若DB=10,CH=4,则DH=14或6.
分析 (1)证明四边形PKCH为菱形,得出PK=HC=PH,即可得出结论;
(2)证明四边形PKCH为菱形,得出PK=PH,即可得出结论;
(3)在(1)(2)的条件下容易得出DH的长.
解答 (1)证明:如图1所示: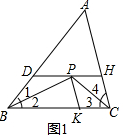
∵PH∥BC,PK∥AC,
∴四边形PKCH是平行四边形,∠2=∠DPB,∠3=∠CPH,
∵∠1=∠2,∠3=∠4,
∴∠1=∠DPB,∠4=∠CPH,
∴BD=DP,PH=HC,
∴四边形PKCH为菱形,
∴PK=HC=PH,
∴DH=DP+PH=BD+HC=BD+PK,
∴BD=DH-PK;
(2)解:图2猜想:BD=DH+PK;理由如下:如图2所示: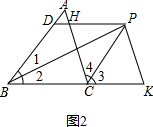 ∵PH∥BC,PK∥AC,
∵PH∥BC,PK∥AC,
∴四边形PKCH是平行四边形,∠2=∠DPB,∠3=∠CPH,
∵∠1=∠2,∠3=∠4,
∴∠1=∠DPB,∠4=∠CPH,
∴BD=DP,PH=HC,
∴四边形PKCH为菱形,
∴PK=PH,
∴DP=DH+PK,
∴BD=DH+PK;
图3猜想:BD=DH-PK;理由如下:如图3所示: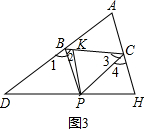
∵PH∥BC,PK∥AC,
∴四边形PKCH是平行四边形,∠2=∠DPB,∠3=∠CPH,
∵∠1=∠2,∠3=∠4,
∴∠1=∠DPB,∠4=∠CPH,
∴BD=DP,PH=HC,
∴四边形PKCH为菱形,
∴PK=PH,
∴DP=DH-PK,
∴BD=DH-PK;
(3)解:在(1)的条件下,
∵CH=PK,BD=DH-PK,
∴DH=BD+CH=10+4=14;
在(2)的条件下,图3同(1)得:DH=14;
图2情况下,∵CH=PK,BD=DH+PK,
∴DH=BD-CH=10-4=6.
故答案为:14或6.
点评 本题考查了菱形的判定与性质、等腰三角形的判定与性质、平行线的性质;证明四边形为菱形是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
19.为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如右:甲:8,7,10,7,8; 乙:9,5,10,9,7.
(1)将下表填写完整;
(2)若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?
(1)将下表填写完整;
| 平 均 数 | 方 差 | |
| 甲 | 8 | 1.2 |
| 乙 | 8 | 3.2 |
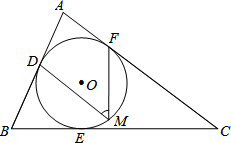 如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.
如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.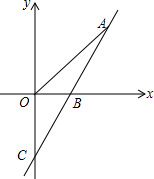 如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
如图,直线y=kx-2与x轴,y轴分别交于点B,C,且OC=2OB,A为直线BC上一动点.
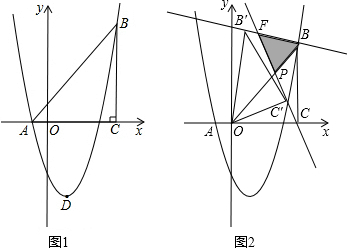
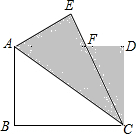 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.