题目内容
20．
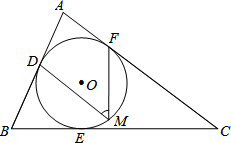如图，⊙O是△ABC的内切圆，点D、E、F为切点，点M为优弧DEF上任意一点，∠B=66°，∠C=37°，求∠M的大小．
分析 连接OD、OF，再利用三角形内角和以及四边形内角和定理求出∠O的度数，进而利用圆周角定理得出∠M的度数．
解答 解：连接OD、OF，
∵E、F均为切点，
∴OD⊥AB，OF⊥AC，
∵∠B=66°，∠C=37°，
∴∠A=180°-∠B-∠C=77°，
∴∠O=360°-∠A-∠ADO-∠AFO=103°，
∵弧DF=弧DF，
∴∠M=$\frac{1}{2}$∠O=51.5°．
点评 此题主要考查了圆周角定理以及切线的性质和四边形内角和定理等知识，得出∠O=103°是解题关键．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
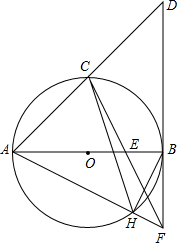如图，AB是⊙O的直径，点C是$\widehat{AB}$的中点，⊙O的切线BD交AC的延长线于点D，E是OB的中点，CE的延长线交切线BD于点F，AF交⊙O于点H，连接BH．
5．已知反比例函数y=$\frac{k}{x}$的图象经过点P（-3，2），则这个函数的图象位于（ ）
| A． | 第二、三象限 | B． | 第一、三象限 | C． | 第三、四象限 | D． | 第二、四象限 |
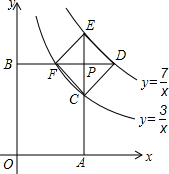如图，过反比例函数y=$\frac{3}{x}$（x＞0）和y=$\frac{7}{x}$（x＞0）的图象之间的点P作两坐标轴的垂线，分别交两坐标轴于点A，B，交两函数图象于点C，E，F，D．若四边形OAPB与四边形CDEF都是正方形，则正方形CDEF的面积为$\frac{8}{5}$．