题目内容
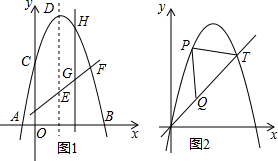
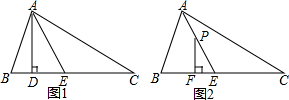
15.如图1,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A、B两点,顶点为D.(1)求b、c的值;
(2)若点E是Rt△ABC斜边AB上一动点(点A、B除外),连接CE,DE,当EC+EO的值最小时,求△BDE的面积;
(3)如图2,连结OB,将△OBC绕点O旋转△OB′C′,直线CC′与直线BB′交于点F,直线CC′与直线OB交于点P,当△BPF是等腰三角形时,直接写出所有点P的坐标.
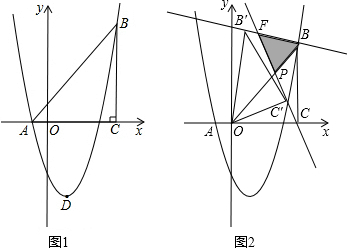
分析 (1)由∠ACB=90°,AC=BC,OA=1,OC=4,可得A(-1,0),B(4,5),C(4,0),然后利用待定系数法即可求得b,c的值;
(2)先根据抛物线的顶点坐标得到D(1,-4),再根据待定系数法得到直线AB的解析式,根据对称性得到点O关于直线AB的对称点为O’(-1,1),根据待定系数法得到直线CO’的解析式,过点D做DF交直线AB于F,可得F(1,2),根据三角形面积公式即可求解;
(3)把△BPF是等腰三角形转化为△CPO是等腰三角形即在直线OB上找一点P使△CPO是等腰三角形,易得P的坐标.
解答 解:(1)∵AC=BC,OA=1,OC=4,
∴A(-1,0),B(4,5),C(4,0),
∵抛物线y=x2+bx+c经过A、B两点.
∴$\left\{\begin{array}{l}{0=1-b+c}\\{25=16+4b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$.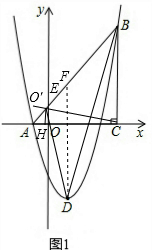 (2)由(1)知y=x2-2x-3=(x-1)2-4,
(2)由(1)知y=x2-2x-3=(x-1)2-4,
所以顶点坐标为D(1,-4),
设直线AB的解析式为y=kx+d,
将A(-1,0),B(4,5)代入y=kx+d,
解得k=1,d=1,
所以直线AB的解析式为y=x+1,
点O关于直线AB的对称点为O′(-1,1).
直线CO′的解析式为y=-0.2x+0.8,
直线AB与直线CO′的交点即为E(-$\frac{1}{6}$,$\frac{5}{6}$),
如图1,过点D作DF交直线AB于F,可得F(1,2),
所以S△DEB=$\frac{1}{2}$DF×CH=$\frac{1}{2}$×6×$\frac{25}{6}$=12.5;
(3)∵△OBC绕点O旋转至△OB′C′,
∴△OCC′,△OB′B是等腰三角形,∠OBB′=∠OCC′,
∴∠B′BO=∠PCO.
∵∠BPF=∠CPO,
∴△BPF∽△CPO,
∴把△BPF是等腰三角形转化为△CPO是等腰三角形.即在直线OB上找一点P使△CPO是等腰三角形.
∵O(0,0),B(4,5),
∴OB直线的解析式为y=$\frac{5}{4}$x.
设P(x,$\frac{5}{4}$x).
①当OP=CP时,有:x2+($\frac{5}{4}$x)2=(4-x)2+($\frac{5}{4}$x)2,解得:x=2,
所以P(2,$\frac{5}{2}$).
②当OP=OC时,有:x2+($\frac{5}{4}$x)2=42,解得:x=±$\frac{16}{41}$$\sqrt{41}$,
所以P($\frac{16}{41}$$\sqrt{41}$,$\frac{20}{41}$$\sqrt{41}$)或P(-$\frac{16}{41}$$\sqrt{41}$,-$\frac{20}{41}$$\sqrt{41}$).
③当CP=OC时,有:(4-x)2+($\frac{5}{4}$x)2=42,解得:x=$\frac{128}{41}$,
所以P($\frac{128}{41}$,$\frac{160}{41}$).
综上所述,P点坐标为(2,$\frac{5}{2}$)或(-$\frac{16}{41}$$\sqrt{41}$,-$\frac{20}{41}$$\sqrt{41}$)或($\frac{16}{41}$$\sqrt{41}$,$\frac{20}{41}$$\sqrt{41}$)或($\frac{128}{41}$,$\frac{160}{41}$).
点评 此题考查了二次函数综合题,涉及了待定系数法求二次函数的解析式,一次函数的解析式,三角形面积问题以及等腰三角形的性质等知识.此题综合性很强,解题的关键是注意方程思想与数形结合思想的应用.

| A. | 第二、三象限 | B. | 第一、三象限 | C. | 第三、四象限 | D. | 第二、四象限 |
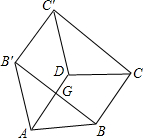 如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.
如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.