题目内容
6.如图1,在平面直角坐标系中,O是坐标原点,矩形OABC在第二象限且A、B、C坐标分别为(-3,0)(-3,$\sqrt{3}$),(0,$\sqrt{3}$),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于点P、Q.(1)如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴时,旋转角α=60°;
(2)在四边形OABC旋转过程中,当0<α≤180°时,存在着这样的点P和点Q,使BP=$\frac{1}{2}$BQ,请直接写出点P的坐标($\frac{-27-\sqrt{105}}{8}$,$\sqrt{3}$)或(-1,$\sqrt{3}$).
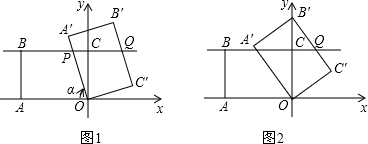
分析 (1)根据正切函数求得∠A′OB′=30°,进而求得α=60°.
(2)在四边形OABC旋转过程中,当0<a≤180°时,存在这样的点P和点Q,使BP=$\frac{1}{2}$BQ;过点Q画QH⊥OA′于H,连接OQ,则QH=OC′=OC,由S△POQ=$\frac{1}{2}$PQ•OC,S△POQ=$\frac{1}{2}$OP•QH,得出PQ=OP;设BP=x,则BQ=2x,当点P在点B左侧时,则OP=PQ=BQ+BP=3x,在Rt△PCO中,根据勾股定理得出(3+x)2+(3)2=(3x)2,解方程即可求得P的坐标,当点P在点B右侧时,OP=PQ=BQ-BP=x,PC=3-x.在Rt△PCO中,根据勾股定理得出(3-x)2+(3)2=x2,解方程即可求得P的坐标.
解答 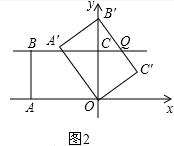 解:(1)如图2,∵矩形OABC在第二象限且A、B、C坐标分别为(-3,0)(-3,$\sqrt{3}$),(0,$\sqrt{3}$),
解:(1)如图2,∵矩形OABC在第二象限且A、B、C坐标分别为(-3,0)(-3,$\sqrt{3}$),(0,$\sqrt{3}$),
∴BC=AO=3,AB=$\sqrt{3}$
∴A′B′=AB=$\sqrt{3}$,OA′=OA=3,
∵B′A′⊥OA′,
∴tan∠A′OB′=$\frac{A′B′}{OA′}$=$\frac{\sqrt{3}}{3}$,
∴∠A′OB′=30°,
∴∠AOA′=90°-30°=60°,
即α=60°.
故答案是:60°.
(2)存在这样的点P和点Q,使BP=$\frac{1}{2}$BQ.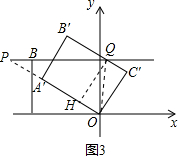
理由如下:过点Q画QH⊥OA′于H,连接OQ,则QH=OC′=OC,
∵S△POQ=$\frac{1}{2}$PQ•OC,S△POQ=$\frac{1}{2}$OP•QH,
∴PQ=OP.
设BP=x,
∵BP=$\frac{1}{2}$BQ,
∴BQ=2x,
如图3,当点P在点B左侧时,
OP=PQ=BQ+BP=3x,
在Rt△PCO中,(3+x)2+($\sqrt{3}$)2=(3x)2,
解得x1=$\frac{3+\sqrt{105}}{8}$,x2=$\frac{3-\sqrt{105}}{8}$,(不符实际,舍去).
∴PC=BC+BP=3+$\frac{3+\sqrt{105}}{8}$=$\frac{27+\sqrt{105}}{8}$,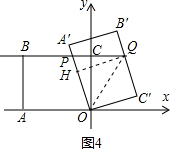
∴P1($\frac{-27-\sqrt{105}}{8}$,$\sqrt{3}$),
如图4,当点P在点B右侧时,
∴OP=PQ=BQ-BP=x,PC=3-x.
在Rt△PCO中,(3-x)2+($\sqrt{3}$)2=x2,解得x=2,
∴PC=BC-BP=3-2=1,
∴P2(-1,$\sqrt{3}$),
综上可知,存在点P1($\frac{-27-\sqrt{105}}{8}$,$\sqrt{3}$),P2(-1,$\sqrt{3}$)使BP=$\frac{1}{2}$BQ.
点评 本题考查了旋转的性质,矩形的性质,勾股定理.特别注意在旋转的过程中的对应线段相等,能够用一个未知数表示同一个直角三角形的未知边,根据勾股定理列方程求解.

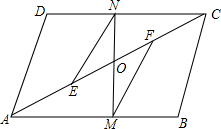 如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分.
如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分. 如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C
如图,已知点A(-3,0)和B(1,0),直线y=kx-4经过点A并且与y轴交于点C