题目内容
19.若a-$\frac{1}{a}$=4,求下列代数式的值:(1)a+$\frac{1}{a}$;
(2)a2-$\frac{1}{{a}^{2}}$;
(3)a2+$\frac{1}{{a}^{2}}$;
(4)a3+$\frac{1}{{a}^{3}}$;
(5)a4+$\frac{1}{{a}^{4}}$;
(6)$\frac{6{a}^{2}}{{a}^{4}+{a}^{2}+1}$.
分析 (1)根据(a+$\frac{1}{a}$)2=(a-$\frac{1}{a}$)2+4,然后开方即可求解;
(2)利用平方差公式变形,然后代入求解;
(3)根据a2+$\frac{1}{{a}^{2}}$=(a-$\frac{1}{a}$)2+2即可代入求解;
(4)利用立方和公式即可代入求解;
(5)根据a4+$\frac{1}{{a}^{4}}$=(a2+$\frac{1}{{a}^{2}}$)2-2,代入求解即可;
(6)首先求得$\frac{{a}^{4}+{a}^{2}+1}{6{a}^{2}}$的值,然后求倒数即可.
解答 解:(1)∵(a+$\frac{1}{a}$)2=(a-$\frac{1}{a}$)2+4=16+4=20,
∴a+$\frac{1}{a}$=±$\sqrt{20}$=±2$\sqrt{5}$;
(2)原式=(a+$\frac{1}{a}$)(a-$\frac{1}{a}$)=±$\sqrt{5}$;
(3)原式=(a-$\frac{1}{a}$)2+2=16+2=18,
(4)原式=(a+$\frac{1}{a}$)(a2+$\frac{1}{{a}^{2}}$-1)=±2$\sqrt{5}$(18-1)=±34$\sqrt{5}$;
(5)原式=(a2+$\frac{1}{{a}^{2}}$)2-2=182-2=322;
(6)$\frac{{a}^{4}+{a}^{2}+1}{6{a}^{2}}$=$\frac{1}{6}$(a2+$\frac{1}{{a}^{2}}$+1)=$\frac{1}{6}$(18+1)=$\frac{19}{6}$.
则原式=$\frac{6}{19}$.
点评 本题考查了代数式的化简求值,正确理解完全平方公式以及立方和公式的结构是关键.

 阅读快车系列答案
阅读快车系列答案| A. | x>$\frac{3}{2}$ | B. | x≥$\frac{3}{2}$ | C. | x<$\frac{3}{2}$ | D. | x≤$\frac{3}{2}$ |
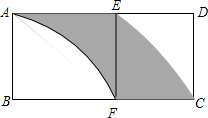 如图,矩形ABCD的长,宽之比为2:1,AF、EC为圆弧,E、F分别为AD、CB的中点,AB=a,求阴影部分的面积.
如图,矩形ABCD的长,宽之比为2:1,AF、EC为圆弧,E、F分别为AD、CB的中点,AB=a,求阴影部分的面积.