题目内容
1.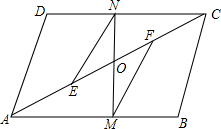 如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分.
如图,?ABCD中,E,F是AC上两点,且AE=CF,又点M,N分别在AB,CD上,且MF∥EN,MN交AC于.求证:EF与MN互相平分.
分析 由四边形ABCD 是平行四边形,得到AB∥CD,根据平行线的性质得到∠1=∠2,因为MF∥EN,得到∠3=∠4,由AE=CF,得出AF=CE,通过△AMF≌△CNE,得到MF=EN,推出四边形EMFN是平行四边形,即可得出结论.
解答 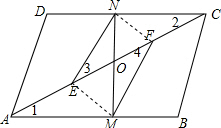 证明:∵四边形ABCD 是平行四边形,
证明:∵四边形ABCD 是平行四边形,
∴AB∥CD,
∴∠1=∠2,
∵MF∥EN,
∴∠3=∠4,
∵AE=CF,
∴AE+EF=CF+EF,
即:AF=CE,
在△AMF与△CNE中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AF=CE}\\{∠4=∠3}\end{array}\right.$,
∴△AMF≌△CNE,
∴MF=EN,
∴四边形EMFN是平行四边形,
∴EF与MN互相平分.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定与性质,熟记平行四边形的判定定理是解题的关键.

练习册系列答案
相关题目
9.若$\sqrt{2x-3}$是二次根式,则x应满足的条件是( )
| A. | x>$\frac{3}{2}$ | B. | x≥$\frac{3}{2}$ | C. | x<$\frac{3}{2}$ | D. | x≤$\frac{3}{2}$ |
 已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.
已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.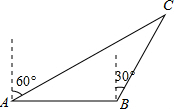 如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?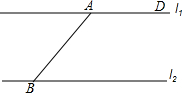 如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.