题目内容
12. 如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )
如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\frac{6\sqrt{13}}{7}$ | D. | $\sqrt{13}$ |
分析 过E作EG⊥AB于G,连接AE,解直角三角形得到∠ABC=30°,根据直角三角形的性质得到AB=4,由等边三角形的性质得到∠CBD=∠DCB=60°,BC=BD,于是得到BF=$\frac{\sqrt{3}}{2}$BC=3,根据旋转的性质得到BE=AB=4,∠EBD=30°,根据勾股定理即可得到结论.
解答 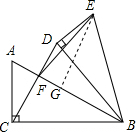 解:过E作EG⊥AB于G,连接AE,
解:过E作EG⊥AB于G,连接AE,
∵CA⊥BC,BC=2$\sqrt{3}$,AC=2,
∴tan∠ABC=$\frac{AC}{BC}=\frac{\sqrt{3}}{3}$,
∴∠ABC=30°,∴AB=4,
∵△BCD是等边三角形,
∴∠CBD=∠DCB=60°,BC=BD,
∴CF⊥AB,BF=$\frac{\sqrt{3}}{2}$BC=3,
∵将△ABC绕点B顺时针旋转得到△EBD,
∴BE=AB=4,∠EBD=30°,
∴∠EBA=60°,
∴BG=$\frac{1}{2}$BE=2,EG=2$\sqrt{3}$,
∴FG=BF-BG=1,
∴EF=$\sqrt{F{G}^{2}+E{G}^{2}}$=$\sqrt{13}$,
故选D.
点评 本题考查的是图形旋转的性质及等边三角形的判定与性质,熟知旋转前、后的图形全等是解答此题的关键.

练习册系列答案
相关题目
2.根据我国《环境空气质量指数AQI技术规定》(试行),AQI共分0-50,51-100,101-150,151-200,201-300和大于300六级,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外运动,如表是某市未来10天的空气质量指数预测:
(1)该市市民在这10天内随机选取1天进行户外运动,求这10天该市市民不适合户外运动的概率;
(2)一名外地游客计划在这10天内到该市旅游,随机选取连续2天游玩,求这10天中适合他旅游的概率.
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQ1 | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(2)一名外地游客计划在这10天内到该市旅游,随机选取连续2天游玩,求这10天中适合他旅游的概率.
7. 如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
 如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )| A. | 68° | B. | 102° | C. | 110° | D. | 112° |
4.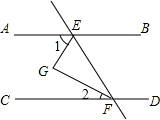 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )| A. | 40° | B. | 35° | C. | 25° | D. | 20° |

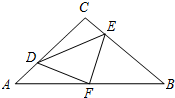 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论: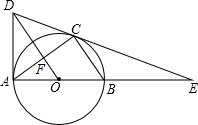 如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.