题目内容
4．
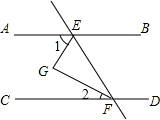如图，直线AB∥CD，EG，FG分别平分∠AEF和∠EFC，如果∠1=70°，那么∠2等于（ ）| A． | 40° | B． | 35° | C． | 25° | D． | 20° |
分析 根据角平分线的定义可得∠1=∠3，∠2=∠4，再根据两直线平行，同旁内角互补列式计算即可得解．
解答 
解：如图，∵EG，FG分别平分∠AEF和∠EFC，
∴∠1=∠3，∠2=∠4，
∵AB∥CD，
∴∠2+∠4=180°-70°×2=40°，
∴∠2=40°÷2=20°．
故选D．
点评 本题考查了平行线的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若物体沿一斜坡下滑（斜坡足够长），它的速度v（m/s）与其下滑t（s）的关系图象如图所示．
如图，AB、CD为两个建筑物，建筑物AB的高度为60米，从建筑物AB的顶部A测得建筑物CD的顶部C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°，则建筑物CD的高度是60-20$\sqrt{3}$米．（结果带根号形式）
12．
如图，等边△BCD中，BC=2$\sqrt{3}$，过C作CA⊥BC，且AC=2，连接AB交CD于点F，将△ABC绕点B顺时针旋转，使得点C与点D重合，得到△EBD，连接FE，则EF的长为（ ）
如图，等边△BCD中，BC=2$\sqrt{3}$，过C作CA⊥BC，且AC=2，连接AB交CD于点F，将△ABC绕点B顺时针旋转，使得点C与点D重合，得到△EBD，连接FE，则EF的长为（ ）| A． | 3$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | $\frac{6\sqrt{13}}{7}$ | D． | $\sqrt{13}$ |
如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC、AC分别交于D、E两点，DF⊥AC于F．
9．
2016年4月15日至5月15日，邯郸市约12万名初三毕业生参加了中考体育测试，为了了解今年初三毕业学生的体育成绩，从某校随机抽取了60名学生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成下面的扇形图和统计表：
请你根据以上图表提供的信息，解答下列问题：
（1）m=24，n=12，x=0.4，y=0.2；
（2）在扇形图中，B等级所对应的圆心角是144度；
（3）请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人？
（4）初三（1）班的甲、乙、丙、丁四人的成绩均为A，现决定从这四名同学中选两名参加学校组织的体育活动，直接写出恰好选中甲、乙两位同学的概率．
2016年4月15日至5月15日，邯郸市约12万名初三毕业生参加了中考体育测试，为了了解今年初三毕业学生的体育成绩，从某校随机抽取了60名学生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成下面的扇形图和统计表：| 等级 | 成绩（分） | 频数（人数） | 频率 |
| A | 27～30 | 21 | 0.35 |
| B | 23～26 | m | x |
| C | 19～22 | n | y |
| D | 18及18以下 | 3 | 0.05 |
| 合计 | 60 | 1.00 |
（1）m=24，n=12，x=0.4，y=0.2；
（2）在扇形图中，B等级所对应的圆心角是144度；
（3）请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人？
（4）初三（1）班的甲、乙、丙、丁四人的成绩均为A，现决定从这四名同学中选两名参加学校组织的体育活动，直接写出恰好选中甲、乙两位同学的概率．
