题目内容
20.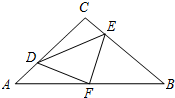 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;
②四边形CDFE的面积保持不变;
③△CDE面积的最大值为8;
④四边形CDFE不可能为正方形;
⑤DE长度的最小值为4.
其中正确的结论是(填序号)???①②③.
分析 ①连接CF,证明△ADF≌△CEF,得到△EDF是等腰直角三角形;
②根据△ADF≌△CEF,得到S四边形CEFD=S△AFC;
③求出DF的最小值,根据当DE最小时,DF也最小进行计算即可;
④根据中点的性质和直角三角形的性质得到四边形CDFE是菱形,利用正方形的判定定理进行判断;
⑤由③的结论进行计算即可.
解答  解:①连接CF,
解:①连接CF,
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB,
∵AD=CE,
∴△ADF≌△CEF,
∴EF=DF,∠CFE=∠AFD,
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形,①正确;
②∵△ADF≌△CEF,
∴S△CEF=S△ADF
∴S四边形CEFD=S△AFC,②正确;
③由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小,
当DF⊥AC时,DE最小,此时DF=$\frac{1}{2}$BC=4.
∴DE=$\sqrt{2}$DF=4$\sqrt{2}$;
当△CEF面积最大时,此时△DEF的面积最小.
此时S△CEF=S四边形CEFD-S△DEF=S△AFC-S△DEF=16-8=8,③正确;
④当D、E分别为AC、BC中点时,CD=DF=FE=EC,
四边形CDFE是菱形,又∠C=90°,
∴四边形CDFE是正方形,④错误;
⑤由③可知当DE最小时,DF也最小,
DF的最小值是4,则DE的最小值为4$\sqrt{2}$,⑤错误,
故答案为:①②③.
点评 本题考查的是正方形的判定、等腰直角三角形的性质、全等三角形的判定和性质,掌握正方形的判定定理、全等三角形的判定定理和性质定理、理解点到直线的距离的概念是解题的关键.

练习册系列答案
相关题目
11.今年第一季度,我省固定资产投资完成475.6亿元,这个数据用科学记数法可表示为( )
| A. | 47.56×109元 | B. | 0.4756×1011元 | C. | 4.756×1010元 | D. | 4.756×109元 |
8.将抛物线y=x2-2x+3向上平移2个单位长度,再向左平移3个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x+2)2+4 | B. | y=(x-4)2+4 | C. | y=(x+2)2 | D. | y=(x-4)2+6 |
12. 如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )
如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )
 如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )
如图,等边△BCD中,BC=2$\sqrt{3}$,过C作CA⊥BC,且AC=2,连接AB交CD于点F,将△ABC绕点B顺时针旋转,使得点C与点D重合,得到△EBD,连接FE,则EF的长为( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\frac{6\sqrt{13}}{7}$ | D. | $\sqrt{13}$ |
9. 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
请你根据以上图表提供的信息,解答下列问题:
(1)m=24,n=12,x=0.4,y=0.2;
(2)在扇形图中,B等级所对应的圆心角是144度;
(3)请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 27~30 | 21 | 0.35 |
| B | 23~26 | m | x |
| C | 19~22 | n | y |
| D | 18及18以下 | 3 | 0.05 |
| 合计 | 60 | 1.00 |
(1)m=24,n=12,x=0.4,y=0.2;
(2)在扇形图中,B等级所对应的圆心角是144度;
(3)请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
10.2015年“十一”黄金周的第二天,北京故宫景点,接待游客超过了最大接待容量,当天接待92 800人次.将92 800用科学记数法表示应为( )
| A. | 928×102 | B. | 92.8×103 | C. | 9.28×104 | D. | 9.28×105 |
 如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,则建筑物CD的高度是60-20$\sqrt{3}$米.(结果带根号形式)
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,则建筑物CD的高度是60-20$\sqrt{3}$米.(结果带根号形式)