题目内容
17.先化简$\frac{{{m^2}-{n^2}}}{{{m^2}-mn}}÷(\frac{n^2}{m}+m+2n)$,再求值,其中|m-1|+(n-2)2=0.分析 先算括号里面的,再算除法,根据非负数的性质求出m、n的值代入进行计算即可.
解答 解:原式=$\frac{(m+n)(m-n)}{mn(m-n)}$÷$\frac{{n}^{2}+{m}^{2}+2mn}{m}$
=$\frac{m+n}{mn}$•$\frac{m}{(m+n)^{2}}$
=$\frac{1}{n(m+n)}$,
∵|m-1|+(n-2)2=0,
∴m-1=0,n-2=0,解得m=1,n=2,
∴原式=$\frac{1}{1+2}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知非负数的性质是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
5.我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
| 图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
| 平移 |  | (1)AB=A′B′,AB∥A′B′ | AA′=BB′ AA′∥BB′ |
| 轴对称 | 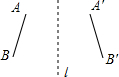 | (2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上. | (3)l垂直平分AA′ |
| 旋转 |  | AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. | (4)OA=OA′,∠AOA′=∠BOB′ |
12. 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数是( )| A. | 22.5° | B. | 36° | C. | 45° | D. | 90° |
2.下列运算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 3$\sqrt{3}$×2$\sqrt{2}$=6$\sqrt{5}$ | C. | 3$\sqrt{5}$÷$\frac{1}{{\sqrt{3}}}$×$\sqrt{3}$=3$\sqrt{5}$ | D. | 3÷$\sqrt{\frac{2}{3}}$=$\frac{3}{2}\sqrt{6}$ |
7.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )
| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2+$\sqrt{3}$或2-$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ |
 如图,点A(1,4),B(-4,a)在双曲线y=$\frac{k}{x}$图象上,直线AB分别交x轴,y轴于C、D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF、BE交于点G.
如图,点A(1,4),B(-4,a)在双曲线y=$\frac{k}{x}$图象上,直线AB分别交x轴,y轴于C、D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF、BE交于点G.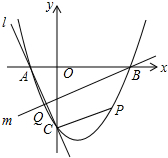 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)
如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)