题目内容
11.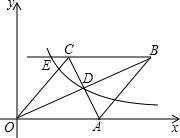 如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:
如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:①双曲线的解析式为y=$\frac{32}{x}$(x>0);
②E点的坐标是(5,8);
③sin∠COA=$\frac{4}{5}$;
④AC+OB=12$\sqrt{5}$.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 过B作BF⊥x轴于点F,由菱形的面积可求得BF,在Rt△ABF中,可求得AF,过D作DG⊥x轴于点G,由菱形的性质可求得D点坐标,则可求得双曲线解析式;根据BC∥OF可知E点纵坐标为BF的长,代入反比例函数的解析式即可得出E点坐标;过C作CH⊥x轴于点H,则HF=BC,可求得OH,可求得sin∠COA;在Rt△OBF中,由勾股定理可求得OB,结合条件可求得AC,则可求得AC+OB,可得出答案.
解答  解:如图,过B作BF⊥x轴于点F,过D作DG⊥x轴于点G,过C作CH⊥x轴于点H,
解:如图,过B作BF⊥x轴于点F,过D作DG⊥x轴于点G,过C作CH⊥x轴于点H,
∵A(10,0),
∴OA=10,
∴S菱形ABCD=OA•BF=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×160=80,即10BF=80,
∴BF=8,
在Rt△ABF中,AB=10,BF=8,由勾股定理可得AF=6,
∴OF=OA+AF=10+6=16,
∵四边形OABC为菱形,
∴D为OB中点,
∴DG=$\frac{1}{2}$BF=$\frac{1}{2}$×8=4,OG=$\frac{1}{2}$OF=$\frac{1}{2}$×16=8,
∴D(8,4),
∵双曲线过点D.
∴4=$\frac{k}{8}$,解得k=32,
∴双曲线解析式为y=$\frac{32}{x}$.
故①正确;
∵BC∥OF,BF=8,
∴y=$\frac{32}{8}$=4,
∴E(4,8).
故②错误;
在Rt△OCH中,OC=10,CH=8,
∴sin∠COA=$\frac{CH}{OC}$=$\frac{8}{10}$=$\frac{4}{5}$,
故③正确;
在Rt△OBF中,OF=16,BF=8,
∴OB=$\sqrt{{OF}^{2}+{BF}^{2}}$=$\sqrt{{16}^{2}+{8}^{2}}$=8$\sqrt{5}$,
∵AC•OB=160,
∴AC=$\frac{160}{OB}$=$\frac{160}{8\sqrt{5}}$=4$\sqrt{5}$,
∴AC+OB=4$\sqrt{5}$+8$\sqrt{5}$=12$\sqrt{5}$,
故④正确;
综上可知正确的为①③④共3个,
故选C.
点评 本题主要考查反比例函数的综合应用,涉及待定系数法、菱形的性质、直角三角形、菱形的面积等知识.利用菱形的面积求得B到x轴的距离是解题的关键,注意菱形两个面积公式的灵活运用.本题考查知识点较基础,综合性很强,但难度不大.

 名校课堂系列答案
名校课堂系列答案 如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠BGE=130°,则∠GEF等于( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
 在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
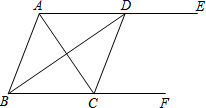 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.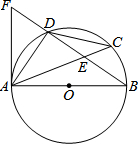 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.