题目内容
2. 在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).(1)求抛物线的表达式;
(2)把-4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
分析 (1)把点(1,0)代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值,从而得到抛物线的表达式;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解答  解:(1)∵二次函数y=x2+mx+2m-7的图象经过点(1,0),
解:(1)∵二次函数y=x2+mx+2m-7的图象经过点(1,0),
∴1+m+2m-7=0,解得m=2.
∴抛物线的表达式为y=x2+2x-3;
(2)y=x2+2x-3=(x+1)2-4.
∵当-4<x<-1时,y随x增大而减小;
当-1≤x<1时,y随x增大而增大,
∴当x=-1,y最小=-4.
当x=-4时,y=5.
∴-4<x<1时,y的取值范围是-4≤y<5;
(3)y=x2+2x-3与x轴交于点(-3,0),(1,0).
新图象M如右图红色部分.
把抛物线y=x2+2x-3=(x+1)2-4的图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=-(x+1)2+4(-3≤x≤1),
当直线y=x+b经过(-3,0)时,直线y=x+b与图象M有两个公共点,此时b=3;
当直线y=x+b与抛物线y=-(x+1)2+4(-3≤x≤1)相切时,直线y=x+b与图象M有两个公共点,
即-(x+1)2+4=x+b有相等的实数解,整理得x2+3x+b-3=0,△=32-4(b-3)=0,解得b=$\frac{21}{4}$.
结合图象可得,直线y=x+b与图象M有三个公共点,b的取值范围是3<b<$\frac{21}{4}$.
点评 本题考查了二次函数图象与几何变换,待定系数法求二次函数的解析式、二次函数的图象和性质,画出函数M的图象是解题的关键.

练习册系列答案
相关题目
12.一次函数y=4x+1,当x>0时,y的取值范围为( )
| A. | y>0 | B. | y<0 | C. | y>1 | D. | 0<y<1 |
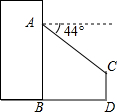 如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
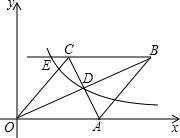 如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:
如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论: