题目内容
1.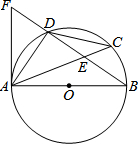 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.(1)求证:AF是⊙O的切线;
(2)若AD=5,AC=8,求⊙O的半径.
分析 (1)欲证明AF是⊙O的切线,只要证明∠FAD+∠DAB=90°,只要证明∠FAD=∠B即可.
(2)先在RT△ADM中求出DM=3,再根据sin∠C=sin∠B=$\frac{3}{5}$=$\frac{AD}{AB}$即可解决问题.
解答 解:(1)证明:∵AB是⊙O的直径,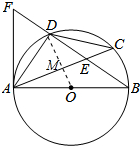
∴∠ADB=90°,
∴AD⊥EF,∠BAD+∠B=90°,
又∵DF=DE,
∴AF=AE,
∴∠FAD=∠EAD,
∵D是$\widehat{AC}$的中点,
∴$\widehat{AD}$=$\widehat{CD}$,
∴∠FAD=∠EAD=∠B,
∴∠FAB=∠FAD+∠BAD=∠BAD+∠B=90°,
∴AF是⊙O的切线.
(2)连接OD交AC于M.
∵$\widehat{AD}$=$\widehat{CD}$,
∴OD⊥AC,AM=CM=$\frac{1}{2}$AC=4,
∴AD=CD=5,
在Rt△DMC中,$DM=\sqrt{C{D^2}-C{M^2}}=3$,$sinC=\frac{DM}{CD}=\frac{3}{5}$,
∵∠B=∠C,
∴$sinB=sinC=\frac{3}{5}$,
∵∠ADB=90°,
∴$AB=\frac{AD}{sinB}=\frac{25}{3}$,
∴⊙O的半径为$\frac{25}{6}$.
点评 本题考查切线的性质、垂径定理、勾股定理、三角函数等知识,解题的关键是灵活运用圆的有关知识,掌握切线的判定方法,属于中考常考题型.

练习册系列答案
相关题目
12.一次函数y=4x+1,当x>0时,y的取值范围为( )
| A. | y>0 | B. | y<0 | C. | y>1 | D. | 0<y<1 |
9.某班派9名同学参加红五月歌咏比赛,他们的身高分别是(单位:厘米):167,159,161,159,163,157,170,159,165.这组数据的众数和中位数分别是( )
| A. | 159,163 | B. | 157,161 | C. | 159,159 | D. | 159,161 |
16.已知关于x的不等式组$\left\{\begin{array}{l}x-a>0\\ 7-2x>1\end{array}\right.$有且只有1个整数解,则a的取值范围是( )
| A. | a>1 | B. | 1≤a<2 | C. | 1<a≤2 | D. | a≤2 |
13.若关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=-4,则m+n的值是( )
| A. | -10 | B. | 10 | C. | -6 | D. | -1 |
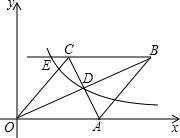 如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:
如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论: