题目内容
20.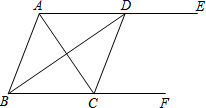 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
分析 (1)根据平行线的性质得出∠ADB=∠DBC,∠DAC=∠BCA,根据角平分线定义得出∠DAC=∠BAC,∠ABD=∠DBC,求出∠BAC=∠ACB,∠ABD=∠ADB,根据等腰三角形的判定得出AB=BC=AD,根据平行四边形的判定得出四边形ABCD是平行四边形,即可得出答案;
(2)先求出BD的长,求出菱形的面积,即可求出答案.
解答 (1)证明:∵AE∥BF,
∴∠ADB=∠DBC,∠DAC=∠BCA,
∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠ACB,∠ABD=∠ADB,
∴AB=BC,AB=AD
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形;
(2)解:过A作AM⊥BC于M,则AM的长是AE,BF之间的距离,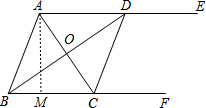
∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
∵AB=5,
∴在Rt△AOB中,由勾股定理得:BO=4,
∴BD=2BO=8,
∴菱形ABCD的面积为$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×6×8=24,
∵四边形ABCD是菱形,
∴BC=AB=5,
∴5×AM=24,
∴AM=$\frac{24}{5}$,
即AE,BF之间的距离是$\frac{24}{5}$.
点评 本题考查了菱形的判定和性质,平行四边形的判定,平行线的性质,等腰三角形的判定的应用,能熟记菱形的判定和性质是解此题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
12.一次函数y=4x+1,当x>0时,y的取值范围为( )
| A. | y>0 | B. | y<0 | C. | y>1 | D. | 0<y<1 |
9.某班派9名同学参加红五月歌咏比赛,他们的身高分别是(单位:厘米):167,159,161,159,163,157,170,159,165.这组数据的众数和中位数分别是( )
| A. | 159,163 | B. | 157,161 | C. | 159,159 | D. | 159,161 |
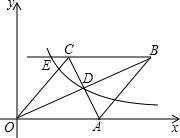 如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:
如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论: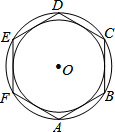 如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为π.
如图,正六边形ABCDEF的边长为2,则该正六边形的外接圆与内切圆所形成的圆环面积为π.