题目内容
6.先化简,后求值:1-$\frac{x-y}{x+2y}$÷$\frac{{x}^{2}{-y}^{2}}{{x}^{2}+4xy+{4y}^{2}}$,其中x=1,y=-2.分析 先算除法,再算加减,把x=1,y=-2代入进行计算即可.
解答 解:原式=1-$\frac{x-y}{x+2y}$•$\frac{(x+2y)^{2}}{(x+y)(x-y)}$
=1-$\frac{x+2y}{x+y}$
=$\frac{x+y-x-2y}{x+y}$
=$\frac{-y}{x+y}$,
当x=1,y=-2时,原式=$\frac{2}{1-2}$=-2.
点评 本题考查的是分式的化简求值,在解答此类问题要把分式的结果化为最简,再把未知数的值代入求解.

练习册系列答案
相关题目
16.初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时.列了如下表格:
根据表格上的信息回答问题:一元二次方程ax2+bx+c=-5的解为( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 3 | 4 | 3 | 0 | -5 | … |
| A. | x1=2,x2=-2 | B. | x1=2,x2=-3 | C. | x1=2,x2=-4 | D. | x1=2,x2=-5 |
18.在四张完全相同的卡片上,分别画有等边三角形、菱形、正五边形、圆.现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
16.已知关于x的不等式组$\left\{\begin{array}{l}x-a>0\\ 7-2x>1\end{array}\right.$有且只有1个整数解,则a的取值范围是( )
| A. | a>1 | B. | 1≤a<2 | C. | 1<a≤2 | D. | a≤2 |
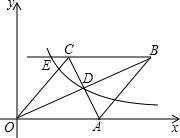 如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论:
如图,在直角坐标系中,四边形OABC为菱形,对角线OB、AC相交于D点,已知A点的坐标为(10,0),双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160(OB>AC),有下列四个结论: