题目内容
因式分解:
(1)x4+2x3+1+2(x+x2)
(2)x4+y4+(x+y)4
(3)(x+1)4+(x2-1)2+(x-1)4.
(1)x4+2x3+1+2(x+x2)
(2)x4+y4+(x+y)4
(3)(x+1)4+(x2-1)2+(x-1)4.
考点:因式分解
专题:
分析:(1)首先重新分组,进而利用十字相乘法以及公式法分解因式进而得出答案;
(2)把前两项配方,第三项展开,整理后利用完全平方公式分解因式即可;
(3)将式子变形为(x+1)4+2(x+1)2(x-1)2+(x-1)4-(x+1)2(x-1)2,根据完全平方公式,平方差公式分解因式即可.
(2)把前两项配方,第三项展开,整理后利用完全平方公式分解因式即可;
(3)将式子变形为(x+1)4+2(x+1)2(x-1)2+(x-1)4-(x+1)2(x-1)2,根据完全平方公式,平方差公式分解因式即可.
解答:解:(1)x4+2x3+1+2(x+x2)
=x4+2x3+x2+x2+2x+1
=x2(x2+2x+1)+(x+1)2
=x2(x+1)2+(x+1)2
=(x+1)2(x2+1);
(2)x4+y4+(x+y)4
=(x2+y2)2-2x2y2+(x2+2xy+y2)2
=(x2+y2)2-2x2y2+(x2+y2)2+4xy(x2+y2)+4x2y2
=2(x2+y2)2+2x2y2+4xy(x2+y2)
=2[(x2+y2)2+x2y2+2xy(x2+y2)]
=2(x2+xy+y2)2;
(3)(x+1)4+(x2-1)2(x-1)4
=(x+1)4+(x+1)2(x-1)2+(x-1)4
=(x+1)4+2(x+1)2(x-1)2+(x-1)4-(x+1)2(x-1)2
=(x+1+x-1)2-(x+1)2(x-1)2
=(2x)2-(x+1)2(x-1)2
=[2x+(x+1)(x-1)][2x-(x+1)(x-1)]
=(x2+2x-1)(x2+2x+1)
=(x+1)2(x2+2x-1).
=x4+2x3+x2+x2+2x+1
=x2(x2+2x+1)+(x+1)2
=x2(x+1)2+(x+1)2
=(x+1)2(x2+1);
(2)x4+y4+(x+y)4
=(x2+y2)2-2x2y2+(x2+2xy+y2)2
=(x2+y2)2-2x2y2+(x2+y2)2+4xy(x2+y2)+4x2y2
=2(x2+y2)2+2x2y2+4xy(x2+y2)
=2[(x2+y2)2+x2y2+2xy(x2+y2)]
=2(x2+xy+y2)2;
(3)(x+1)4+(x2-1)2(x-1)4
=(x+1)4+(x+1)2(x-1)2+(x-1)4
=(x+1)4+2(x+1)2(x-1)2+(x-1)4-(x+1)2(x-1)2
=(x+1+x-1)2-(x+1)2(x-1)2
=(2x)2-(x+1)2(x-1)2
=[2x+(x+1)(x-1)][2x-(x+1)(x-1)]
=(x2+2x-1)(x2+2x+1)
=(x+1)2(x2+2x-1).
点评:考查了利用分组分解法进行因式分解,难度较大,利用配方和完全平方公式,平方差公式整理是解题的关键.

练习册系列答案
相关题目
若3x3-kx2+4被3x-1除后余3,则k的值为( )
| A、2 | B、4 | C、9 | D、10 |
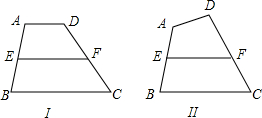
 已知y+2与x成正比例,且x=-2时,y=0.
已知y+2与x成正比例,且x=-2时,y=0. 如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.
如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.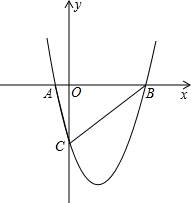 如图,在△ABC中,点A在x轴负半轴上,点B在x轴正半轴上,AB=6,点C在y轴负半轴上,且OC=5,抛物线y=a(x-2)2+k经过△ABC的三个顶点.
如图,在△ABC中,点A在x轴负半轴上,点B在x轴正半轴上,AB=6,点C在y轴负半轴上,且OC=5,抛物线y=a(x-2)2+k经过△ABC的三个顶点.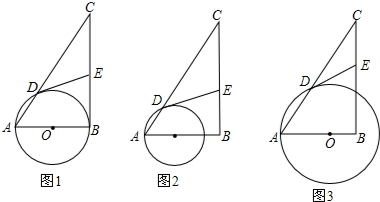
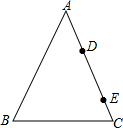 如图,在△ABC中,D、E为边AC上的两个点,试在AB,BC上各取一个点M,N,使四边形DMNE的周长最短.
如图,在△ABC中,D、E为边AC上的两个点,试在AB,BC上各取一个点M,N,使四边形DMNE的周长最短.