题目内容
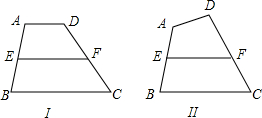
(1)①如图Ⅰ,在梯形ABCD中,AD∥BC,E,F分别是AB,CD的中点,连接EF,证明:EF=
(AD+BC);
②如图Ⅱ,在四边形ABCD中,若AD与BC不平行,E,F分别是AB、CD的中点,连接EF,判断EF与
(AD+BC)的大小关系,并说明理由.
③综合①、②可得结论:在任意四边形ABCD中,若E,F分别是AB、CD的中点,则EF与
(AD+BC)的大小关系是 ;
(2)从(1)的①到③,我们将“梯形ABCD”改为“四边形ABCD”后进行的探索,实际上就是一个“一般化”的过程---将梯形两腰中点连线的性质“一般化”成任意四边形一组对比中点连线的性质.请将命题“菱形的面积等于它的两条对角线的积的一半”一般化后探索新的结论,并说明理由(友情提醒:命题“菱形的面积等于它的两条对角线的积的一半”不需证明)
| 1 |
| 2 |
②如图Ⅱ,在四边形ABCD中,若AD与BC不平行,E,F分别是AB、CD的中点,连接EF,判断EF与
| 1 |
| 2 |
③综合①、②可得结论:在任意四边形ABCD中,若E,F分别是AB、CD的中点,则EF与
| 1 |
| 2 |
(2)从(1)的①到③,我们将“梯形ABCD”改为“四边形ABCD”后进行的探索,实际上就是一个“一般化”的过程---将梯形两腰中点连线的性质“一般化”成任意四边形一组对比中点连线的性质.请将命题“菱形的面积等于它的两条对角线的积的一半”一般化后探索新的结论,并说明理由(友情提醒:命题“菱形的面积等于它的两条对角线的积的一半”不需证明)

考点:四边形综合题,梯形中位线定理
专题:综合题
分析:(1)①证明:连接AC,取AC的中点G,如图Ⅰ,先根据三角形中位线性质得到EG∥BC,EG=
BC,GF∥AD,GF=
AD,由于AD∥BC,利用平行线的性质得EG∥BC,GF∥BC,根据过直线外一点有且只有一条直线与已知直线平行,得到点G在EF上,于是有EF=EG+GF=
(AD+BC);
②如图Ⅱ,连接AC,取AC的中点G,连接GE、GF,与①一样得到EG∥BC,EG=
BC,GF∥AD,GF=
AD,由于AD与BC不平行,根据平行线的性质得点G不在EF上,
则根据三角形三边的关系得到EF<GF+GE,则EF<
(AD+BC);
③利用①②得,在任意四边形ABCD中,当E,F分别是AB、CD的中点,EF≤
(AD+BC).
(2)探索新的结论为:若四边形的两条对角线互相垂直,则四边形的面积等于对角线乘积的一半.利用三角形面积公式进行证明.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②如图Ⅱ,连接AC,取AC的中点G,连接GE、GF,与①一样得到EG∥BC,EG=
| 1 |
| 2 |
| 1 |
| 2 |
则根据三角形三边的关系得到EF<GF+GE,则EF<
| 1 |
| 2 |
③利用①②得,在任意四边形ABCD中,当E,F分别是AB、CD的中点,EF≤
| 1 |
| 2 |
(2)探索新的结论为:若四边形的两条对角线互相垂直,则四边形的面积等于对角线乘积的一半.利用三角形面积公式进行证明.
解答:(1)①证明:连接AC,取AC的中点G,如图Ⅰ,

∵E,F分别是AB,CD的中点,
∴EG为△ABC的中位线,GF为△CAD的中位线,
∴EG∥BC,EG=
BC,GF∥AD,GF=
AD,
∵AD∥BC,
∴EG∥BC,GF∥BC,
∴E、G、F三点共线,即点G在EF上,
∴EF=EG+GF=
BC+
AD=
(AD+BC);
②EF<
(AD+BC).理由如下:
如图Ⅱ,连接AC,取AC的中点G,连接GE、GF,

与①一样可得EG∥BC,EG=
BC,GF∥AD,GF=
AD,
∵AD与BC不平行,
∴EG与GF不共线,即点G不在EF上,
∴EF<GF+GE,
∴EF<
AD+
BC,
即EF<
(AD+BC);
③由①②得,在任意四边形ABCD中,当E,F分别是AB、CD的中点,EF≤
(AD+BC).
故答案为EF≤
(AD+BC).
(2)若四边形的两条对角线互相垂直,则四边形的面积等于对角线乘积的一半.理由如下:
如图3,四边形ABCD的对角线AC与BD相交于O点,且AC⊥BD,

则S四边形ABCD=S△ABD+S△CBD
=
•OA•BD+
•OC•BD
=
•BD(OA+OC)
=
•BD•AC.

∵E,F分别是AB,CD的中点,
∴EG为△ABC的中位线,GF为△CAD的中位线,
∴EG∥BC,EG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD∥BC,
∴EG∥BC,GF∥BC,
∴E、G、F三点共线,即点G在EF上,
∴EF=EG+GF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②EF<
| 1 |
| 2 |
如图Ⅱ,连接AC,取AC的中点G,连接GE、GF,

与①一样可得EG∥BC,EG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD与BC不平行,
∴EG与GF不共线,即点G不在EF上,
∴EF<GF+GE,
∴EF<
| 1 |
| 2 |
| 1 |
| 2 |
即EF<
| 1 |
| 2 |
③由①②得,在任意四边形ABCD中,当E,F分别是AB、CD的中点,EF≤
| 1 |
| 2 |
故答案为EF≤
| 1 |
| 2 |
(2)若四边形的两条对角线互相垂直,则四边形的面积等于对角线乘积的一半.理由如下:
如图3,四边形ABCD的对角线AC与BD相交于O点,且AC⊥BD,

则S四边形ABCD=S△ABD+S△CBD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查了四边形的综合题:熟练掌握梯形的性质、梯形的中位线性质和三角形中位线性质;会运用三角形三边的关系判断线段之间的大小关系;在学习数学的过程中,勇于探索从特殊到一般的变化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
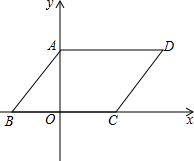 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB. 如图,已知AB为弦,MC为切线,BM⊥AB,求证:AC∥DM.
如图,已知AB为弦,MC为切线,BM⊥AB,求证:AC∥DM.