题目内容
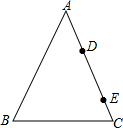 如图,在△ABC中,D、E为边AC上的两个点,试在AB,BC上各取一个点M,N,使四边形DMNE的周长最短.
如图,在△ABC中,D、E为边AC上的两个点,试在AB,BC上各取一个点M,N,使四边形DMNE的周长最短.考点:轴对称-最短路线问题
专题:
分析:以AB为轴作D的对称点D′,以BC为轴作E点的对称点E′,连接D′E′,交AB、BC于M、N,连接DM、EN,则四边形DMNE即为所求.
解答: 解:以AB为轴作△ABC的对称三角形ABP,则D关于AB的对称点D′在AP上,以BC为轴作△ABC的对称三角形KBC,则E关于BC的对称点E′在CK上,连接D′E′,交AB、BC于M、N,连接DM、EN,则DM+MN+EN=D′M+MN+E′N=D′E′,所以四边形DMNE的周长最短;
解:以AB为轴作△ABC的对称三角形ABP,则D关于AB的对称点D′在AP上,以BC为轴作△ABC的对称三角形KBC,则E关于BC的对称点E′在CK上,连接D′E′,交AB、BC于M、N,连接DM、EN,则DM+MN+EN=D′M+MN+E′N=D′E′,所以四边形DMNE的周长最短;
 解:以AB为轴作△ABC的对称三角形ABP,则D关于AB的对称点D′在AP上,以BC为轴作△ABC的对称三角形KBC,则E关于BC的对称点E′在CK上,连接D′E′,交AB、BC于M、N,连接DM、EN,则DM+MN+EN=D′M+MN+E′N=D′E′,所以四边形DMNE的周长最短;
解:以AB为轴作△ABC的对称三角形ABP,则D关于AB的对称点D′在AP上,以BC为轴作△ABC的对称三角形KBC,则E关于BC的对称点E′在CK上,连接D′E′,交AB、BC于M、N,连接DM、EN,则DM+MN+EN=D′M+MN+E′N=D′E′,所以四边形DMNE的周长最短;点评:此题主要考查了轴对称最短路线应用以及轴对称的性质,得出M、N点位置是解题关键.

练习册系列答案
相关题目
下列命题中,正确的是( )
| A、过弦的中点的直线平分弦所对的弧 |
| B、过弦的中点的直线必经过圆心 |
| C、弦所对的两条弧的中点的连线垂直平分弦,且过圆心 |
| D、弦的垂线平分弦所对的弧 |
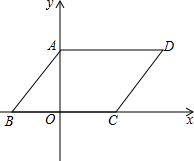 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB. 要把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形.
要把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形.