题目内容
13.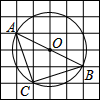 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )| A. | $\frac{\sqrt{5}}{2}$π | B. | $\frac{\sqrt{5}}{4}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
分析 由AB、BC、AC长可推导出△ACB为等腰直角三角形,连接OC,得出∠BOC=90°,计算出OB的长就能利用弧长公式求出$\widehat{BC}$的长了.
解答 解:∵每个小方格都是边长为1的正方形,
∴AB=$2\sqrt{5}$ AC=$\sqrt{10}$ BC=$\sqrt{10}$,
∴AC2+BC2=AB2,
∴△ACB为等腰直角三角形,
∴∠A=∠B=45°,
∴连接OC,则∠COB=90°,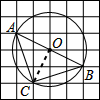
∵OB=$\sqrt{5}$
∴$\widehat{BC}$的长为:$\frac{90•π•\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}π$
故选:A.
点评 本题考查了弧长的计算以及圆周角定理,解题关键是利用三角形三边长通过勾股定理逆定理得出△ACB为等腰直角三角形.

练习册系列答案
相关题目
4.下列运算中,计算正确的是( )
| A. | x2y÷y=x2 | B. | (2x2)3=6x5 | C. | (-π)0=0 | D. | a6÷a3=a2 |
5. 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )| A. | (1,$\frac{5}{2}$) | B. | ($\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\sqrt{5}$,2$\sqrt{5}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$) |
3.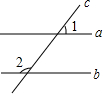 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
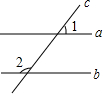 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )| A. | 157°62′ | B. | 137°22′ | C. | 137°62′ | D. | 47°22′ |
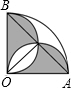 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)