题目内容
5. 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )| A. | (1,$\frac{5}{2}$) | B. | ($\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\sqrt{5}$,2$\sqrt{5}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$) |
分析 根据相似三角形对应边成比例求出CB、AC的关系,从而得到$\frac{CB}{AB}$=$\frac{1}{3}$,过点C作CD⊥y轴于点D,然后求出△AOB和△CDB相似,根据相似三角形对应边成比例求出CD、BD,再求出OD,最后写出点C的坐标即可.
解答  解:∵A(-4,0),B(0,2),
解:∵A(-4,0),B(0,2),
∴OA=4,OB=2,
∵△COB∽△CAO,
∴$\frac{CB}{CO}$=$\frac{CO}{AC}$=$\frac{OB}{OA}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴CO=2CB,AC=2CO,
∴AC=4CB,
∴$\frac{CB}{AB}$=$\frac{1}{3}$,
过点C作CD⊥y轴于点D,
∵AO⊥y轴,
∴AO∥CD,
∴△AOB∽△CDB,
∴$\frac{CD}{AO}$=$\frac{DB}{OB}$=$\frac{CB}{AB}$=$\frac{1}{3}$,
∴CD=$\frac{1}{3}$AO=$\frac{4}{3}$,
BD=$\frac{1}{3}$OB=$\frac{2}{3}$,
∴OD=OB+BD=2+$\frac{2}{3}$=$\frac{8}{3}$,
∴点C的坐标为($\frac{4}{3}$,$\frac{8}{3}$).
故选B.
点评 本题考查了相似三角形的性质,坐标与图形性质,主要利用了相似三角形对应边成比例,求出$\frac{CB}{AB}$=$\frac{1}{3}$是解题的关键,也是本题的难点.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
16. 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )| A. | $\frac{31}{2}$,15 | B. | 15,$\frac{31}{2}$ | C. | 15,15 | D. | $\frac{31}{2}$,$\frac{31}{2}$ |
13.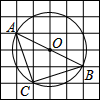 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )| A. | $\frac{\sqrt{5}}{2}$π | B. | $\frac{\sqrt{5}}{4}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
17.下列说法中,正确的是( )
| A. | 任何一个数都有平方根 | B. | 任何正数都有两个平方根 | ||
| C. | 算术平方根一定大于0 | D. | 一个数不一定有立方根 |
15.两年前生产1吨甲种药品的成本是5000元.随着生产技术的进步,成本逐年下降,第2年的年下降率是第1年的年下降率的2倍,现在生产1吨甲种药品成本是2400元.为求第一年的年下降率,假设第一年的年下降率为x,则可列方程( )
| A. | 5000(1-x-2x)=2400 | B. | 5000(1-x)2=2400 | ||
| C. | 5000-x-2x=2400 | D. | 5000(1-x)(1-2x)=2400 |
 如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.
如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.