题目内容
8.为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,请完成下列问题:(1)周三没有被选择的概率;
(2)选择2天恰好为连续两天的概率.
分析 (1)画树状图展示所有20种等可能的结果数,再找出周三没有被选择的结果数,然后根据概率公式求解;
(2)找出选择2天恰好为连续两天的结果数,然后利用概率公式求解.
解答 解:(1)画树状图为:
共有20种等可能的结果数,周三没有被选择的结果数12,
所以周三没有被选择的概率=$\frac{12}{20}$=$\frac{3}{5}$;
(2)选择2天恰好为连续两天的结果数为8,
所以选择2天恰好为连续两天的概率=$\frac{8}{20}$=$\frac{2}{5}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
19.下列图案中,可以看作是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16. 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )| A. | $\frac{31}{2}$,15 | B. | 15,$\frac{31}{2}$ | C. | 15,15 | D. | $\frac{31}{2}$,$\frac{31}{2}$ |
3.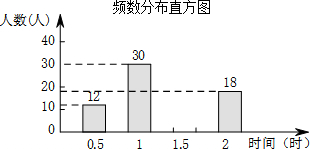 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
某校七年级部分同学的劳动时间频数分布表
(1)求m的值,并补全频数分布直方图.
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
 在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:某校七年级部分同学的劳动时间频数分布表
| 劳动时间(时) | 频数 |
| 0.5 | 12 |
| 1 | 30 |
| 1.5 | m |
| 2 | 18 |
| 合计 | 100 |
(2)被调查同学劳动时间的中位数是1.5小时.
(3)求被调查同学的平均劳动时间.
13.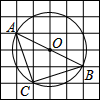 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )| A. | $\frac{\sqrt{5}}{2}$π | B. | $\frac{\sqrt{5}}{4}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
17.下列说法中,正确的是( )
| A. | 任何一个数都有平方根 | B. | 任何正数都有两个平方根 | ||
| C. | 算术平方根一定大于0 | D. | 一个数不一定有立方根 |
 如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°.
如图,⊙O为△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,D为⊙O上一点,∠ABC=∠ODC=67.5°. 如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.
如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.