题目内容
1.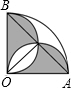 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
分析 过点C作CD⊥OB,CE⊥OA,则△AOB是等腰直角三角形,由∠ACO=90°,可知△AOC是等腰直角三角形,由HL定理可知Rt△OCE≌Rt△ACE,故可得出S扇形OEC=S扇形AEC,$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{AC}$与弦AC所围成的弓形面积,S阴影=S△AOB即可得出结论.
解答  解:过点C作CD⊥OB,CE⊥OA,
解:过点C作CD⊥OB,CE⊥OA,
∵OB=OA,∠AOB=90°,
∴△AOB是等腰直角三角形,
∵OA是直径,
∴∠ACO=90°,
∴△AOC是等腰直角三角形,
∵CE⊥OA,
∴OE=AE,OC=AC,
在Rt△OCE与Rt△ACE中,
∵$\left\{\begin{array}{l}{OC=AC}\\{OE=AE}\end{array}\right.$,
∴Rt△OCE≌Rt△ACE(HL),
∵S扇形OEC=S扇形AEC,
∴$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{AC}$与弦AC所围成的弓形面积,
同理可得,$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{BC}$与弦BC所围成的弓形面积,
∴S阴影=S△AOB=$\frac{1}{2}$×1×1=$\frac{1}{2}$cm2.
故答案是:$\frac{1}{2}$cm2.
点评 本题考查的是扇形面积的计算与等腰直角三角形的判定与性质,根据题意作出辅助线,构造出直角三角形得出S阴影=S△AOB是解答此题的关键.

练习册系列答案
相关题目
11.某商场将进货价为每只30元的台灯以每只40元售出,平均每月能售出600只.调查表明,这种台灯的售价每上涨1元,其销售量将减少10只.当这种台灯的售价定为多少元时,每个月的利润恰为10 000元?
16. 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
 某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )
某校男子足球队的年龄分布如下面的条形统计图,则这些队员年龄的众数和中位数分别是( )| A. | $\frac{31}{2}$,15 | B. | 15,$\frac{31}{2}$ | C. | 15,15 | D. | $\frac{31}{2}$,$\frac{31}{2}$ |
13.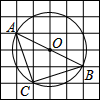 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆⊙O,则$\widehat{BC}$的长等于( )| A. | $\frac{\sqrt{5}}{2}$π | B. | $\frac{\sqrt{5}}{4}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
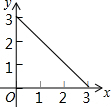
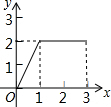
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )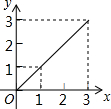
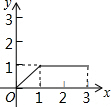
 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是($\frac{6}{5}$,$\frac{11}{5}$),则k的值为8.
如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是($\frac{6}{5}$,$\frac{11}{5}$),则k的值为8.