题目内容
2.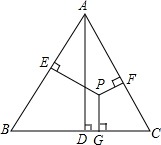 如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.
如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.
分析 连接PA、PB、PC,根据△ABP、△BCP、△ACP的面积和等于△ABC的面积,由等边三角形的三边相等,即可得出结论.
解答 解:连接PA、PB、PC,如图所示: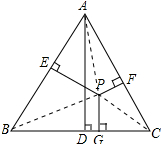
∵S△ABP+S△BCP+S△ACP=S△ABC,
∴$\frac{1}{2}$AB•PE+$\frac{1}{2}$BC•PD+$\frac{1}{2}$AC•PF=$\frac{1}{2}$BC•AD,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴$\frac{1}{2}$BC(PE+PF+PG)=$\frac{1}{2}$BC•AD,
∴PE+PD+PF=AD.
点评 本题主要考查了等边三角形的性质以及三角形面积的计算方法;通过作辅助线,根据三角形面积相等得出结论是常用的方法.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.一组数据:2,4,5,6,x的平均数是4,则这组数的方差是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 10 | D. | $\sqrt{10}$ |
17.已知函数y=$\left\{{\begin{array}{l}{-x+6(x≤2)}\\{2x(x>2)}\end{array}}$,则当函数值y=8时,自变量x的值是( )
| A. | -2或4 | B. | 4 | C. | -2 | D. | ±2或±4 |
7.若a=2016,b=-2017,则分式1+$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$÷$\frac{1}{a}$的值是( )
| A. | 2016 | B. | 0 | C. | -2017 | D. | 4034 |
14.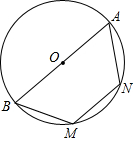 如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )
如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )
 如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )
如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )| A. | 3 | B. | 5 | C. | 3$\sqrt{2}$ | D. | 6 |
 如图,已知四边形ABCD是边长为4cm的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F,当∠EOD=30°时,CE的长是$\sqrt{21}$.
如图,已知四边形ABCD是边长为4cm的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F,当∠EOD=30°时,CE的长是$\sqrt{21}$.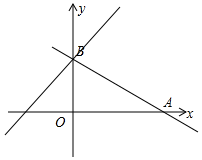 如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.
如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.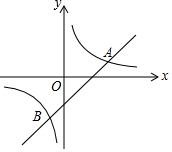 如图,直线y=x-2与反比例函数y=$\frac{k}{x}$的图象交于点A(3,1)和点B.
如图,直线y=x-2与反比例函数y=$\frac{k}{x}$的图象交于点A(3,1)和点B.