题目内容
11.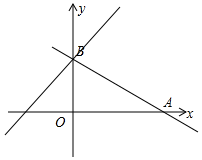 如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.
如图,已知一次函数y=-$\frac{1}{2}$x+3的图象与x轴、y轴分别交于点A、B.(1)求点A,B两点的坐标.
(2)点M为一次函数y=x+3的图象上一点,若△ABM与△ABO的面积相等,求点M的坐标.
(3)点Q为y轴上的一点,若△ABQ为等腰三角形,请直接写出Q点坐标.
分析 (1)对于直线y=-$\frac{1}{2}$x+3,令x=0得到y=3,令=0得到x=6,可得A(6,0),B(0,3).
(2)如图1中,作OM∥AB交直线y=x+3于M,求出直线OM的解析式,利用方程组可得点M的坐标,再利用中线的性质求出M′的坐标即可.
(3)分种情形分别讨论即可解决问题.
解答 解:(1)对于直线y=-$\frac{1}{2}$x+3,令x=0得到y=3,令=0得到x=6,
∴A(6,0),B(0,3).
(2)如图1中,作OM∥AB交直线y=x+3于M,
∵OM∥AB,
∴S△ABM=S△ABO,
∵直线AB的解析式为y=-$\frac{1}{2}$x+3,
∴直线OM的解析式为y=-$\frac{1}{2}$x,
由$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{y=x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,
∴点M的坐标为(-2,1).
当BM=BM′时,△ABM′与△ABM的面积相等,此时M′(2,5),
∴满足条件的点M的坐标为(-2,1)或(2,5).
(3)如图2中,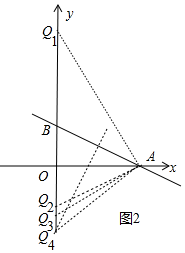
在Rt△ABO中,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=3$\sqrt{5}$,
当BA=BQ时,点Q的坐标为(0,3+3$\sqrt{5}$)或(0,3-3$\sqrt{5}$),
当AB=AQ时,点Q的坐标为(0,-3),
当QB=QA时,设QA=QB=a,在Rt△AOQ中,∵OA2+OQ2=AQ2,
∴(a-3)2+62=a2,
解得a=$\frac{15}{2}$,
∴OQ=BQ-OB=$\frac{9}{2}$,
∴点Q的坐标为(0,-$\frac{9}{2}$).
综上所述,满足条件的点Q的坐标为(0,3+3$\sqrt{5}$)或(0,3-3$\sqrt{5}$)或(0,-3)或(0,-$\frac{9}{2}$).
点评 本题考查一次函数综合题、三角形的面积、平行线的性质、等腰三角形的判定和性质等知识,今天的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会构建一次函数,利用方程组确定两个函数的交点坐标,属于中考压轴题.

| A. | ${C_{13}}^5$ | B. | ${C_{13}}^6$ | C. | ${C_{13}}^{11}$ | D. | ${C_{12}}^7$ |
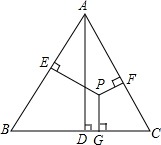 如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.
如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG. 如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.
如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为3$\sqrt{2}$.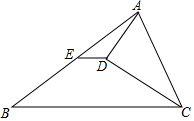 已知,如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证:
已知,如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证: