题目内容
14.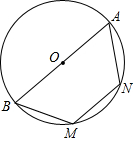 如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )
如图,AB是⊙O的直径,M,N是⊙O上的两点,且AN=3,∠M=120°,则⊙O的半径为( )| A. | 3 | B. | 5 | C. | 3$\sqrt{2}$ | D. | 6 |
分析 连接BN,如图,先利用圆内接四边形的性质得到∠A=60°,再利用圆周角定理得到∠ANB=90°,则∠ABN=30°,然后根据含30度的直角三角形三边的关系得到AB的长,从而得到⊙O的半径.
解答 解:连接BN,如图,
∵∠M+∠A=180°,
∴∠A=180°-120°=60°,
∵AB为直径,
∴∠ANB=90°,
∴∠ABN=30°,
∴AB=2AN=6,
∴⊙O的半径为3.
故选A.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
4.化简$\frac{m-1}{m}$÷$\frac{1-m}{m^2}$是( )
| A. | m | B. | -m | C. | $\frac{1}{m}$ | D. | -$\frac{1}{m}$ |
5.已知实数x,y满足(x-$\sqrt{{x}^{2}-2016}$)(y-$\sqrt{{y}^{2}-2016}$)=2016,则3x2-2y2+3x-3y-2015的值为( )
| A. | -2016 | B. | 2016 | C. | -1 | D. | 1 |
6.已知“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,若公式 Cnm=$\frac{n!}{m!(n-m)!}$(n>m),则C125+C126=( )
| A. | ${C_{13}}^5$ | B. | ${C_{13}}^6$ | C. | ${C_{13}}^{11}$ | D. | ${C_{12}}^7$ |
4.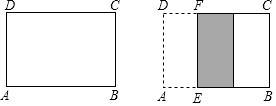 如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).
如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).
填写下列表格:
 如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).
如图,在长方形纸片ABCD中,AB=15cm,AD=10cm.将纸片沿EF折叠,EF∥AD,设AE=x(cm),折叠后重叠部分的面积为S(cm2).填写下列表格:
| x/cm | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| S/cm2 | 10 | 30 | 50 | 70 | 60 | 40 | 20 |
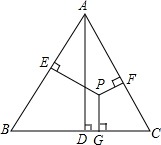 如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.
如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.