题目内容
5．若分式方程$\frac{x-6}{x-5}=\frac{k}{5-x}$（其中k为常数）产生增根，则k=1．分析 增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．把增根代入化为整式方程的方程即可求出k的值．
解答 解：方程两边都乘（x-5），得
x-6=-k，
∵原方程有增根，
∴x-5=0，
解得x=5，
∴把x=5代入整式方程，得k=1．
故答案为1．
点评 本题考查了分式方程的增根，增根确定后可按如下步骤进行：
①化分式方程为整式方程；
②把增根代入整式方程即可求得相关字母的值．
练习册系列答案
名师点拨卷系列答案
相关题目
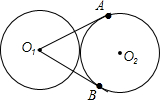如图，两个等圆⊙O1和⊙O2外切，过点O1作⊙O2的两条切线OA、OB，A、B为切点，则∠AO1B=60°．
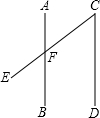如图，AB∥CD，∠AFE=125°，则∠C的度数为55°．
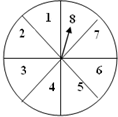自由转动如图所示的转盘．下列事件中哪些是必然事件？那些是随机事件？根据你的经验，将这些事件的序号按发生的可能性从小到大的顺序排列．
10．
如图，平面直角坐标系中，△ABC的顶点坐标分别是A（-3，1），B（-1，1），C（-2，2），当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时，b的取值范围是（ ）
如图，平面直角坐标系中，△ABC的顶点坐标分别是A（-3，1），B（-1，1），C（-2，2），当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时，b的取值范围是（ ）| A． | -1≤b≤$\frac{1}{2}$ | B． | -1≤b≤1 | C． | -$\frac{1}{2}$≤b≤1 | D． | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
17．估计与$\sqrt{11}$最接近的整数是（ ）
| A． | 3 | B． | 4 | C． | -3 | D． | ±3 |
阅读下列材料：已知，$\sqrt{2^2}=2$，$\sqrt{{{（{-2}）}^2}}=2$，$\sqrt{3^2}=3$，$\sqrt{{{（{-3}）}^2}}=3$，$\sqrt{4^2}=4$，$\sqrt{{{（{-4}）}^2}}=4$，$\sqrt{0^2}=0$，…