题目内容
15.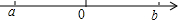 阅读下列材料:已知,$\sqrt{2^2}=2$,$\sqrt{{{({-2})}^2}}=2$,$\sqrt{3^2}=3$,$\sqrt{{{({-3})}^2}}=3$,$\sqrt{4^2}=4$,$\sqrt{{{({-4})}^2}}=4$,$\sqrt{0^2}=0$,…
阅读下列材料:已知,$\sqrt{2^2}=2$,$\sqrt{{{({-2})}^2}}=2$,$\sqrt{3^2}=3$,$\sqrt{{{({-3})}^2}}=3$,$\sqrt{4^2}=4$,$\sqrt{{{({-4})}^2}}=4$,$\sqrt{0^2}=0$,…(1)从上述等式可以得出结论$\sqrt{a^2}=\left\{\begin{array}{l}\_\_\_\_\_\_\_\_\_\_\_(a≥0)\\ \_\_\_\_\_\_\_\_\_\_\_(a<0)\end{array}\right.$
(2)实数a,b在数轴上的位置如图所示,请用上述结论化简$\sqrt{a^2}+\sqrt{b^2}-|b|$.
分析 (1)由题意知非负数平方得算术平方根是其本身,负数的平方得算术平方根是其相反数;
(2)先由数轴上a,b两点的位置,判断出a,b的符号,再利用(1)中结论化简即可.
解答 解:(1)由题意知,$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a}&{a≥0}\\{-a}&{a<0}\end{array}\right.$;
(2)由数轴可知,a<0,b>0,
∴$\sqrt{a^2}+\sqrt{b^2}-|b|$=-a+b-b=-a.
点评 本题考查了绝对值、二次根式的性质、实数与数轴,关键是熟悉二次根式的性质.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
10.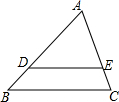 如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
 如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )
如图,在△ABC中,AB=4,AC=3,DE∥BC交AB于点D,交AC于点E,若AD=3,则AE的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{4}{9}$ |
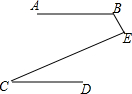 如图,AB∥CD,∠B=125°,∠C=23°,则∠E的度数为78°.
如图,AB∥CD,∠B=125°,∠C=23°,则∠E的度数为78°.